8 Intervals

We already learned about half steps and whole steps, which are types of intervals. In this chapter, we will learn about the most basic types of intervals.

8.1  INTERVAL NUMBERS

An interval is the distance between two notes. Half steps and whole steps are types of intervals. When we first learned how to write scales, we used a sequence of half steps and whole steps. Although half steps and whole steps are technically intervals, we use very specific labels when identifying intervals. Interval labels contain two parts.

We will first focus on the interval number. Being able to quickly identify and write the interval number will save you a great deal of time.

For the interval number, always count the bottom note as “1” and count up, alternating between lines and spaces. For example, a diatonic half step and a diatonic whole step both have the interval number of “2,” which we call a “second.”

Example 8.1.1. Seconds

A shows a second is from C5 to D5. B shows a second is also when D descends to C. A and B are melodic intervals. C is a harmonic interval from B to C. D and E show incorrect ways to write a second.

The intervals in Example 8.1.1 are seconds because there are two notes and the distance between the two notes is a second. Examples 8.1.1A, B, and C are correctly written but Examples 8.1.1D and E are incorrectly written.

  • Example 8.1.1A: This is a melodic second because the notes are played separately. The second ascends.
  • Example 8.1.1B: This melodic second descends.
    • Notice that the C is still considered “1,” while the D is considered “2.” This is because intervals are always based on the lowest note.
  • Example 8.1.1C: This is a harmonic second because the notes are performed at the same time.
    • Harmonic interval: when an interval is played simultaneously. Another name for a two-note harmonic interval is a dyad.
    • This time, because B is the lowest note, B is considered “1,” while C is now “2.”
    • In order to not confuse melodic intervals with harmonic ones, be sure to put enough space in between melodic intervals.
    • Notice how the harmonic second is written. Because both noteheads cannot fit directly above one another, they must be staggered as shown. The lower note always goes on the left. Think: Lower Left.
  • Example 8.1.1D: This harmonic second is incorrectly written.
    • The notes are not staggered and are extremely difficult to distinguish when they overlap.
  • Example 8.1.1E: This harmonic second is incorrectly written because the lower note is on the right.
    • Remember that the lower note of the dyad must be on the left.[1]

As previously mentioned, it does not matter if the second is a half step or a whole step. As long as the notes are a second apart, the interval is called a second. Observe the following examples, which are all seconds.

Example 8.1.2. More seconds

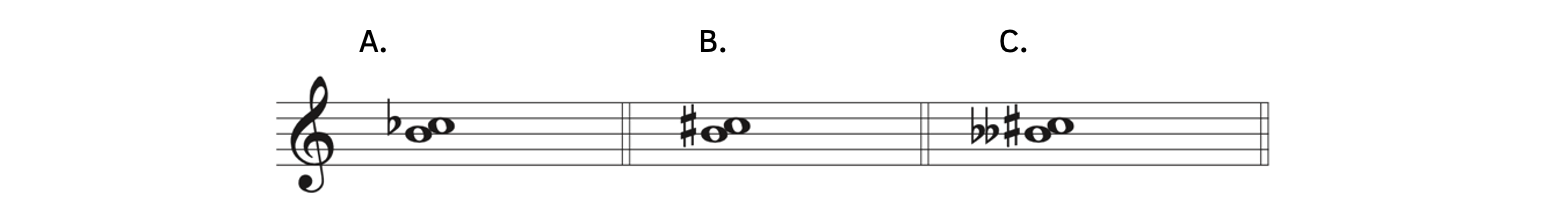
Three examples of seconds, although their accidentals are always different. A shows B and C-flat; B shows B and C-sharp; C shows B-double-flat and C-sharp.

  • Example 8.1.2A: C-flat is enharmonically equivalent to B. However, because the note names B and C are a second part, this interval is a second.
  • Example 8.1.2B: Even though this example is different from Example 8.1.2A because of the C-sharp, it is also a second.
  • Example 8.1.2C: This example is extreme. The distance from B-double-flat to C-sharp is four half steps. However, since the note names B and C are only a second apart, this interval is a second.

The top line of Rothschild’s “Si j’étais Rayon” illustrates several seconds (Example 8.1.3).

Example 8.1.3. Seconds in Rothschild[2], “Si j’étais Rayon”

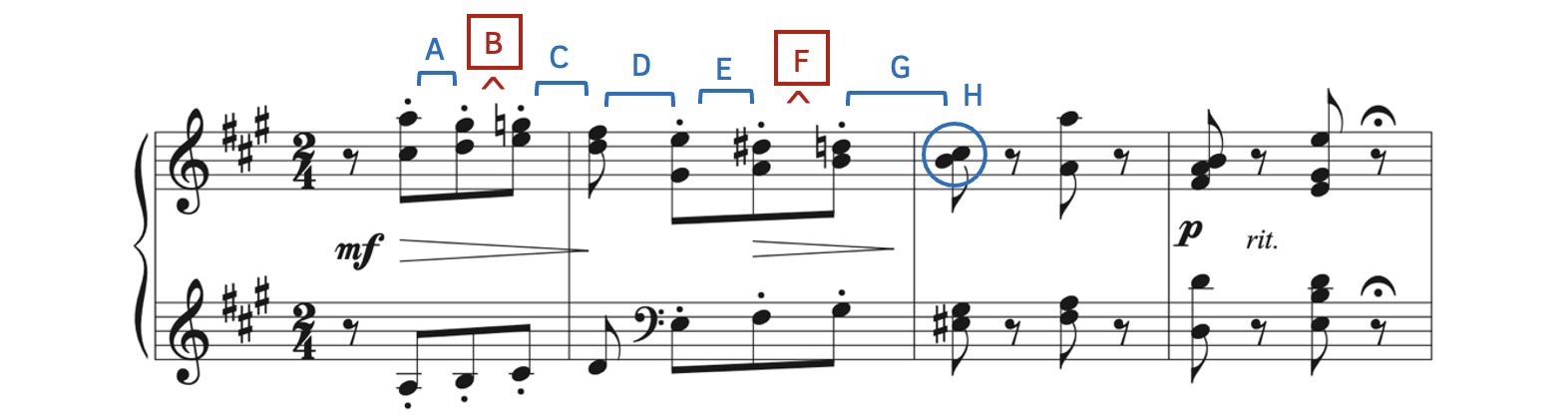
There are a number of seconds in Rothschild's Se j'etais Rayon. Two are not seconds.

There is a combination of melodic and harmonic seconds, and some intervals are not seconds.

  • Square brackets in blue represent melodic seconds (Examples 8.1.3A, C, D, E, and G).
    • Most seconds in this example are half steps (Examples 8.1.3A, C, E, and G), but one second is a whole step (Example 8.1.3D).
  • Red boxes symbolize intervals that are not seconds (Examples 8.1.3B and F).
    • Although Examples 8.1.3B and F are half steps, they are chromatic half steps (and not diatonic half steps). Because the note names are the same, they cannot be seconds.
    • For example, Example 8.1.3B connects G-sharp to G-natural. The distance from G to G is not a second; therefore, the interval from G-sharp to G-natural is not a second.
  • There is one harmonic second found at Example 8.1.3H. Notice how the second is written, with the lower note on the left.

Example 8.1.4 shows all the different interval numbers from 1–8 written as harmonic intervals.

Example 8.1.4. Interval numbers

Interval numbers are listed: 1-unison, 2-second, 3-third, 4-fourth, 5-fifth, 6-sixth, 7-seventh, and 8-octave.

The first row of Arabic numerals is how we label the interval and the second row shows how we say the interval. Most intervals are called by their ordinal numbers (second, third, fourth) with two exceptions: the unison and the octave. They are never called the first and the eighth. Notice the following characteristics in Example 8.1.4:

  • The third to the octave stack neatly above one another. However, the unison and second are written differently.
    • Harmonic unison whole notes must have two noteheads next to each other in order to tell that there are two notes. If there is only one notehead, it is assumed that there is only one note.
    • Harmonic seconds must be written side by side because the top note does not neatly fit above. The lower note is always to the left.
  • When the bottom note is in a space, all the odd-numbered intervals are in spaces of the staff. If the bottom note were on a line, all odd-numbered intervals would be on lines.
    • Shortcut! Knowing that odd-numbered intervals are in the same space/line as the bottom note will help you quickly identify and write intervals.
  • All even-numbered intervals are on lines because the bottom note is in a space.

Sometimes composers will choose to use a variety of intervals in the melody, such as in Berg’s Lyric Suite (Example 8.1.5).

Example 8.1.5. Variety of intervals: Berg[3], Lyric Suite, i – Allegretto gioviale

The opening violin line in Berg's Lyric Suite goes through every interval.

In Example 8.1.5, the interval numbers appear above the staff in between notes. What do you notice above the interval numbers? Berg takes advantage of every interval number from 1 (the unison) to 8 (the octave). Compare Berg’s variety of interval numbers to Rothchild’s use of steps (mostly seconds) in Example 8.1.3. Neither is stronger or better—each musical composition will have its own unique characteristics.

Interval Numbers

When counting interval numbers, always be sure to count the bottom note first and include it when you count. Even though C to D is only a step apart, it is called a second (2) because you count C (1) up to D (2).

Accidentals

When writing harmonic seconds, the notes had to be staggered because there was not enough room to fit both notes. Similarly, when writing harmonic intervals where both notes have accidentals, the accidentals must be staggered in a specific order when there is not enough room. For melodic intervals, this is not an issue since the accidentals will simply be written before each note.

Example 8.1.6. Order of accidentals

A shows that for intervals a seventh or larger, accidentals are aligned directly above one another. B shows that for intervals a sixth or smaller, the closer accidental is placed next to the higher note and the bottom note's accidental is farther away.

  • Example 8.1.6A: For harmonic intervals a seventh or larger, align the accidentals directly above one another. This is possible because with the larger intervals, the accidentals will not overlap each other.
  • Example 8.1.6B: For harmonic intervals a sixth or smaller, stagger the accidentals. Do not align the accidentals directly above one another because they will overlap if you write the accidentals correctly.
    • Write the accidental closer to the higher note.
    • Write the accidental farther away from the lower note.

Example 8.1.7 illustrates the correct way (and several incorrect ways) to write accidentals.

Example 8.1.7. Writing accidentals

Example A shows the correct way to write accidentals where the higher note's accidental is closer and the lower note's accidental is farther away. Examples B, C, and D are incorrectly written. Example E shows a melodic interval.

  • Example 8.1.7A: This shows the correct way to stagger accidentals. Notice that the sharp is placed more closely to the higher note, B, and that the sharps are not aligned.
  • Example 8.1.7B: The accidentals are incorrectly placed, as the bottom note has the closer accidental.
  • Example 8.1.7C: The accidentals are incorrectly placed, as they are aligned but the interval is only a fourth. Notice how difficult it is to read the accidentals when they overlap.
  • Example 8.1.7D: The accidentals seem to fit aligned, but are too tiny. Have mercy on the eyes of your theory professor.
  • Example 8.1.7E: The accidentals for melodic intervals do not require any special rules. These accidentals are correctly written.

Example 8.1.8 illustrates how accidentals should be written for dyads up to an octave.

Example 8.1.8. Accidentals

Accidentals are shown correctly on all harmonic intervals from a unison to an octave.

  • For the unison, although there are two whole notes to show that there are two simultaneous F-flats, there is only one accidental.
    • A second flat placed next to the flat would look like a double flat.
    • A second flat placed in between the two notes would look like a melodic interval.
  • For intervals from seconds to sixths, the accidentals are staggered.
    • The top note always receives the closer accidental, while the accidental for the bottom note sits farther away.
  • For intervals a seventh or larger, the accidentals are aligned because they can fit without overlapping.

Some accidentals such as the double sharp are smaller, so two double sharps can fit directly above one another for smaller intervals. For now, just be sure that accidentals do not overlap because they can be difficult to read.

Wieck Schumann’s Caprice illustrates how accidentals are placed before harmonic dyads of different sizes (Example 8.1.9).

Example 8.1.9. Placement of accidentals in Wieck Schumann[4], Caprice, Op. 2, No. 6

Placement of accidentals are shown in real music in Wieck Schumann's Caprice, Op. 2, No. 6

Notice that accidentals are aligned or staggered:

  • Example 8.1.9A: Because the interval is an octave, there is enough space to comfortably align the two flats directly above one another.
  • Examples 8.1.9B and C: This time, the intervals are only a third. For smaller intervals, the higher note receives the closer accidental and the lower note’s accidental is placed farther away. The accidentals are not aligned.

Accidentals

  • For intervals a sixth or smaller, stagger accidentals so the higher note gets the closer accidental.
  • For intervals a seventh or larger, align accidentals.

 

Practice 8.1A

Directions:

  • Identify the interval number as quickly as possible.

Identify the interval number. 1 - b up to G. 2 - B up to D. 3 - B up to B. 4 - B up to F. 5 - B to the same B. 6 - G up to B. 7 - E up to B. 8 - E down to E. 9 - D up to E. 10 - A up to D. 11 - F down to A. 12 - B up to C. 13 - G up to F. 14 - B up to E. 15 - F up to F. 16 - E up to C. 17 - G up to B.

Click here to watch the tutorial.

Solution
1) 6
2) 3
3) 8
4) 5
5) 1
6) 3
7) 5
8) 8
9) 2
10) 4
11) 6
12) 2
13) 7
14) 4
15) 8
16) 6
17) 3

Practice 8.1B

Directions:

  • Write harmonic intervals above the given notes using whole notes. Add sharps to both notes.

Write harmonic intervals above the given notes using whole notes. Add sharps to both notes. 1 through 5 are in treble clef. 1- fifth above F. 2 - second above F. 3 - fourth above F. 4 - seventh above F. 5 - unison with F. Numbers 6 through 11 are in bass clef. 6 - Octave above B. 7 - Sixth above C. 8 - Third above G. 9 - Seventh above E. 10 - Fifth above D. 11 - Sixth above A. Numbers 12 through 14 are in alto clef. 12 - Second above A. 13 - Seventh above B. 14 - Unison with E. Last 3 are in tenor clef. 15 - Octave above E. 16 - Fifth above B. 17 - Fourth above A.

Click here to watch the tutorial.

Practice 8.1C

Directions:

  • Identify the interval number for the circle intervals below.

Rothschild, “Les Papillons”

Intervals circled to be identified in Rothschild's Les Papillons

Click here to watch the tutorial.

Solution
1) 3
2) 5
3) 8
4) 4
5) 8
6) 6
7) 6
8) 7

8.2  INTERVALS IN THE MAJOR SCALE

In the last section, we learned that interval labels have two parts: interval quality and interval number. In order to learn the interval qualities, it is helpful to think of them in relation to the major scale and natural minor scale. This technique will also help you in aural training, when you are asked to sing and identify intervals.

Example 8.2.1 shows all the intervals based on the tonic within a major scale.

Example 8.2.1. Intervals in the major scale

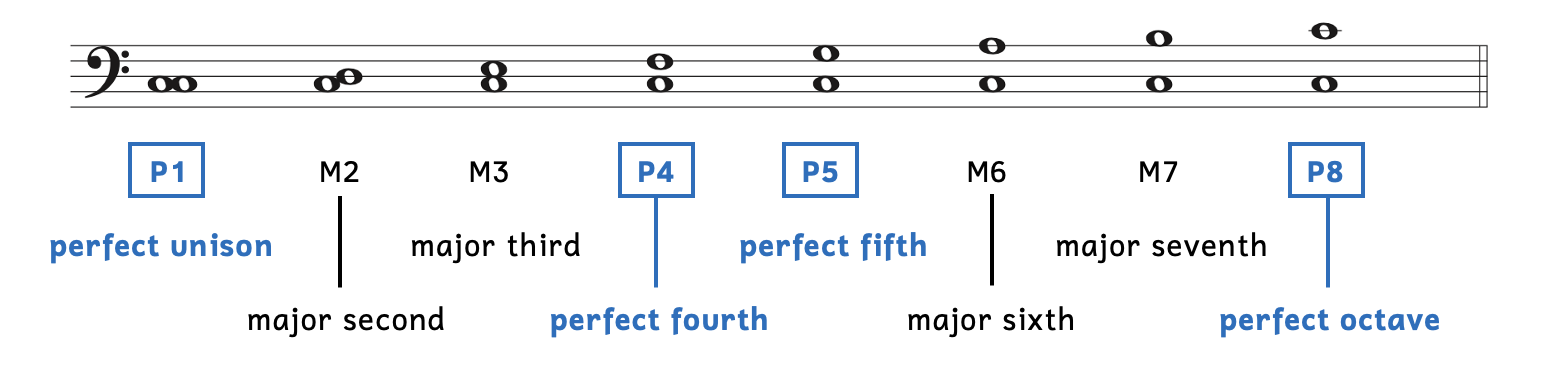
The intervals created from a major scale are the perfect octave, major second, major third, perfect fourth, perfect fifth, major sixth, major seventh, and perfect octave. The perfect unison, perfect fourth, perfect fifth, and perfect octave are boxed.

The first row shows how we label the interval and the bottom two rows show how we say the intervals.

  • The intervals in blue boxes (unison, fourth, fifth, and octave) are perfect intervals (P).
    • The perfect intervals are so named because the unison, fifth, and octave have the purest sounds. Historically, music for two voices could only begin with a unison, fifth, or octave and end with a unison or octave.
    • The fourth being labeled as perfect is a convenience, as we will later learn.
  • The other intervals (second, third, sixth, and seventh) are major intervals (M).
    • The major intervals are easy to remember because they all belong to the major key.

Perfect intervals and major intervals are never interchangeable. In other words, the third can never be perfect and the fourth can never be major.

When a major key signature is given, identifying intervals is simple if you have the interval qualities memorized. For example, the third will always be major and the fourth will always be perfect. Notice that in Example 8.2.2, which is in E-flat major, the interval qualities are the same as in Example 8.2.1. Again, this is because the interval qualities are always the same in any major scale.

Example 8.2.2. Intervals in the E-flat major scale

The same intervals are in the E-flat major scale as in the C major scale from Example 8.2.1.

We can rewrite Example 8.2.2 using accidentals and without a key signature (Example 8.2.3).

Example 8.2.3. Intervals in the E-flat major scale without a key signature

The intervals are the same whether there is a key signature of not if it is in a major key. The notes in Example 8.2.3 are the same as those in Example 8.2.2.

Notice that the notes and intervals in Example 8.2.3 are exactly the same as Example 8.2.2. Because the accidentals are the same, the intervals are the same. Observe the intervals found in Beach’s “Peace I Leave With You,” which is also in E-flat major (Example 8.2.4).

Example 8.2.4. Intervals in Beach[5], “Peace I Leave With You”

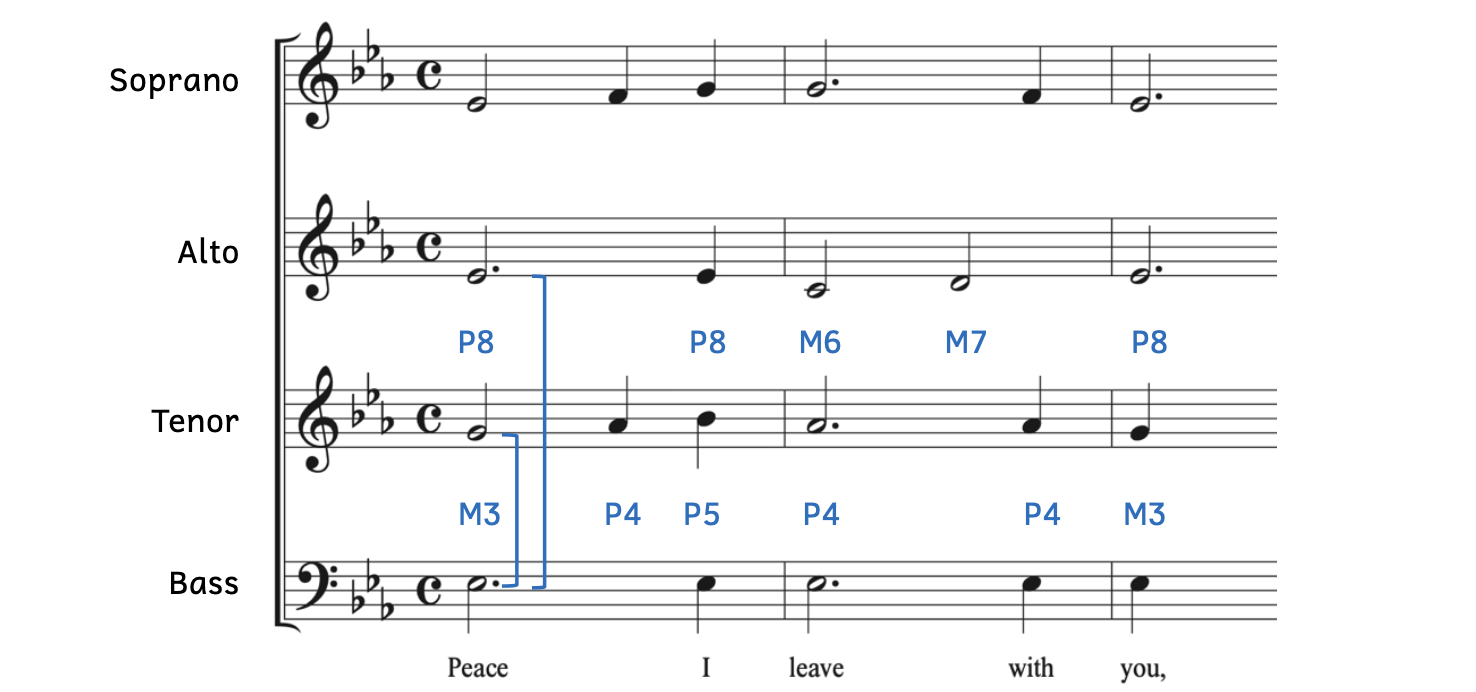
The intervals have been written in for Beach's "Peace I Leave With You." All the intervals belong to the major key.

Remember that intervals are always based on the lowest note. In Example 8.2.4, the bass has the lowest note, E-flat3. Because the other voices (soprano, alto, and tenor[6]) are higher than the bass, the intervals are based on the bass’s E-flat3. Since the key is E-flat major and E-flat is the lowest note, all the intervals will belong to the E-flat major scale.

In Example 8.2.4, the intervals between the alto and bass and the intervals between the tenor and bass are shown. Notice that all the intervals are either major or perfect, just like they were in Example 8.2.1 to Example 8.2.3. The intervals between the soprano and bass are not shown because the distance is greater than an octave. Intervals greater than an octave will be covered in Chapter 9 (More Intervals).

Intervals in the Major Scale

Based on any given major key signature, the intervals above the tonic will always be the following:

  • P1, P4, P5, P8
  • M2, M3, M6, M7

Identifying Intervals

Here are the steps to follow when asked to identify intervals.

Example 8.2.5. Identify the given intervals:

Three intervals are shown to be identified. Example A is G up to E; Example B is F up to B-flat. And Example C is F-sharp up to A-sharp.

Step one: Write in the interval number.

Example 8.2.6. Step one

Interval numbers are shown. Example A is a sixth. Example B is a fourth. Example C is a third.

Step two: Ask yourself if the top note belongs to the major key of the bottom note. If so, the quality is either major or perfect, depending on the interval number.

Example 8.2.7. Step two

The answers are given. Example A is a major sixth. Example B is a perfect fourth. Example C is a major third.

  • Example 8.2.7A:
    • The bottom note is G.
    • The key signature of G major has one sharp (F-sharp), so E belongs to the key of G major.
    • Therefore, E is a major sixth (M6) above G because the interval is a sixth and E belongs to the key of G major.
  • Example 8.2.7B:
    • The bottom note is F.
    • The key signature of F major has one flat (B-flat), so B-flat belongs to the key of F major.
    • Therefore, B-flat is a perfect fourth (P4) above F because the interval is a fourth and B-flat belongs to the key of F major.
  • Example 8.2.7C:
    • The bottom note is F-sharp.
    • The key signature of F-sharp major has six sharps (F-sharp, C-sharp, G-sharp, D-sharp, A-sharp, E-sharp), so A-sharp belongs to the key of F-sharp major.
    • Therefore, A-sharp is a major third (M3) above F-sharp because the interval is a third and A-sharp belongs to the key of F-sharp major.

In Example 8.2.8, the melodic intervals between each note are shown. All the intervals are from the major scale except for the one marked as “X.”

Example 8.2.8. Melodic Intervals in Abrams[7], “A Smile and a Tear”

Intervals are shown between notes in Abrams, "A Smile and a Tear". Specific intervals are given in the text below.

Remember that intervals are always based on the lower note. For melodic intervals, examine each pair of notes and think in the key of the lower note. Identify the interval number, then see if the higher note belongs in the major key of the lower note.

  • Example 8.2.8A: This is a perfect unison (P1) because the note repeats.
  • Example 8.2.8B: The lower note is F and C is a fifth above F. Because F major has one flat (B-flat), C belongs to F major. Therefore, the interval from F to C is a perfect fifth (P5).
    • Even though the first note was C, it was not the lower note.
  • Example 8.2.8C: The interval from F up to A is a major third (M3).
  • Example 8.2.8D: The lower note is G and A is a second above G. Because G major has only one sharp (F-sharp), A exists in G major. Therefore, the interval from A to G is a major second (M2).
  • Example 8.2.8E: The interval from G down to F is a major second (M2).
    • G major has one sharp (F-sharp). However, the lower note is F and not G. We must think in the key of the lower note (F) and G exists in F major.
  • Example 8.2.8F: The interval from F up to B-flat is a perfect fourth (P4) since F major has one flat (B-flat).
  • Example 8.2.8G: The lower note is B-flat and D is a third above B-flat. Because the key of B-flat major has two flats (B-flat and E-flat), D does not have a flat and belongs to the B-flat major scale. Therefore, the interval from B-flat to D is a major third (M3).
  • Example 8.2.8H: The lower note is D and F is a third above D. The key of D major has two sharps (F-sharp and C-sharp). However, the next note is not F-sharp, but F-natural. Therefore, the interval between D and F does not belong to the D major scale and is represented with an “X.” We will learn about this interval later in the chapter.
  • Example 8.2.8I: The lower note is C and F is a fourth above C. Because C major has no sharps or flats, F is a perfect fourth (P4) above C.

Identifying Intervals

  1. Write in the interval number.
  2. If the top note belongs to the major scale of the bottom note, the interval is either major or perfect.

Writing Intervals

Here are the steps to follow when asked to write given intervals.

Example 8.2.9. Write the following harmonic intervals above the given notes.

Write the intervals above the given notes. Example A asks for a major seventh above A. Example B asks for a perfect fifth above E-flat. Example C asks for a major second above B.

Step one: Write in the pitch based solely on the interval number (without an accidental).

Example 8.2.10. Step one

Example A shows that a generic seventh above A is G. Example B shows that a generic fifth above E-flat is B. Example C shows that a generic second above B is C.

  • Example 8.2.10A: A seventh above A is G. Because A is in a space, the seventh above (an odd number) will also be in a space.
  • Example 8.2.10B: A fifth above E-flat is B. Because E-flat is on a line, the fifth above (an odd number) will also be on a line.
  • Example 8.2.10C: A second above B is C. For seconds, do not forget to place the notes staggered side by side, with the lower note to the left.

Step two: Add any necessary accidentals to the top note so that it belongs to the bottom note’s major key.

Example 8.2.11. Step two

Example A shows that G-sharp is a major seventh above A. Example B shows that B-flat is a perfect fifth above E-flat. Example C shows that C-sharp is a major second above B.

  • Example 8.2.11A:
    • Because the key signature of A major has three sharps (F-sharp, C-sharp, and G-sharp), add a sharp to G.
    • G-sharp is a major seventh (M7) above A because it belongs to the key of A major.
  • Example 8.2.11B:
    • Because the key signature of E-flat major has three flats (B-flat, E-flat, and A-flat), add a flat to B.
    • B-flat is a perfect fifth (P5) above E-flat because it belongs to the key of E-flat major.
    • Notice that the flats are staggered and not written directly above one another. If the flats are not staggered, the flats are too small.
  • Example 8.2.11C:
    • Because the key signature of B major has five sharps (F-sharp, C-sharp, G-sharp, D-sharp, and A-sharp), add a sharp to C.
    • C-sharp is a major second (M2) above B because it belongs to the key of B major.
    • We learned how harmonic seconds should be written. Notice that the sharp is outside the second, and not in between B and C.

Writing Intervals

  1. Write in the pitch solely based on the interval number (without an accidental).
  2. Add any necessary accidentals to the top note so that it belongs to the major key of the bottom note.

Practice 8.2A

Directions:

  • Identify the interval based on the major key of the bottom note. If the interval does not belong to the major key, write an “X.”

Number 1, G-flat up to F-flat. Number 2, G-flat up to B-flat. Number 3, G-flat up to C-flat. Number 4, G-flat up to G. Number 5, G-flat up to A-flat. Number 6, F up to B. Number 7, D up to C-sharp. Number 8, D down to B-flat. Number 9, A-flat up to E-flat. Number 10, F-sharp up to D. Number 11, E-flat down to D.

Click here to watch the tutorial.

Solution
1) X
2) M3
3) P4
4) X
5) M2
6) X
7) M7
8) M3
9) P5
10) X
11) X

Practice 8.2B

Directions:

  • Based on the given interval, write the pitch above the given note.
    • For #1-9, write melodic intervals using half notes.
    • For #10-15, write harmonic intervals using whole notes.

Number 1, major sixth above B. Number 2, perfect fifth above B. Number 3, perfect fourth above B. Number 4, major second above B. Number 5, major third above D. Number 6, perfect unison to D-flat. Number 7, major seventh above C-sharp. Number 8, perfect fourth above F-sharp. Number 9, perfect octave above C-flat. Number 10, perfect fourth above G. Number 11, perfect seventh above B-flat. Number 12, perfect unison to F. Number 13, major second above E. Number 14, perfect octave above C-sharp. Number 15, major third above D-flat.

Click here to watch the tutorial.

Practice 8.2C

Directions:

  • Identify all the intervals between the bass and upper voices. In this case, the “bass” is Alto #2 and the upper voices are Soprano #1, Soprano #2, and Alto #1. Write the intervals between Soprano #1 and Alto #2; Soprano #2 and Alto #2; and Alto #1 and Alto #2. A sample has been given.

Reichardt[8], “Weihnachten: Welche Morgenröten wallen” (“Christmas: What Dawns Wave”)

Number 1, D up to D. Number 2, D up to C-sharp. Number 3, D up to B. Number 4, D up to C-sharp. Number 5, D up to D. Number 6, D up to A. Number 7, D up to G. Number 8, D up to F-sharp. Number 9, D up to A. Number 10, D up to E. Number 11, D up to F-sharp. Number 11, D to D. Number 13, D up to F-sharp.

Click here to watch the tutorial.

Solution
1) P8
2) M7
3) M6
4) M7
5) P8
6) P5
7) P4
8) M3
9) P5
10) M2
11) M3
12) P1
13) M3

8.3  SHORTCUT: P4/P5

Although it would be helpful to quickly identify and write all the intervals, there are a few intervals that you will use more often. The ability to quickly identify and write the perfect intervals will come in handy. What do you notice about the following perfect intervals?

Example 8.3.1. Perfect intervals

Example A, G-flat to G-flat is a perfect unison. Example B, F-sharp to F-sharp is a perfect octave. Example C, B-flat to E-flat is a perfect fourth. Example D, C-sharp to G-sharp is a perfect fifth.

All the pairs of notes in Example 8.3.1 share the same accidentals.

  • Example 8.3.1A: Perfect unisons will clearly share the same accidentals all the time, since they are the same pitch.
  • Example 8.3.1B: Perfect octaves will also share the same accidentals all the time, because they are the same note, but an octave apart.
  • Example 8.3.1C: Perfect fourths will always share the same accidentals, except for the notes F and B. The notes here are B-flat and E-flat. The lower note is B-flat and B-flat’s key signature has two flats (B-flat and E-flat). Therefore, E has a flat.
  • Example 8.3.1D: Perfect fifths will always share the same accidentals, except for the notes B and F. The notes here are C-sharp and G-sharp. The lower note is C-sharp and C-sharp’s key signature contains all seven sharps. Therefore, G has a sharp.

Because the perfect unison and perfect octave always share the same accidentals, we will focus on the perfect fourth and perfect fifth.

Example 8.3.2. Perfect fourth and perfect fifth

Example A, A to D is a perfect fourth. Example B, A-flat to D-flat is a perfect fourth. Example C, F to C is a perfect fifth. Example D, F-sharp to C-sharp is a perfect fifth.

  • Example 8.3.2A:
    • The bottom note does not have an accidental and the interval number is 4.
    • The notes are not F and B.
    • Therefore, the top note also does not have an accidental.
    • Check: The key signature of A major has three sharps (F-sharp, C-sharp, and G-sharp); D does not have a sharp.
  • Example 8.3.2B:
    • The bottom note has a flat and the interval number is 4.
    • The notes are not F and B.
    • Therefore, the top note also has a flat.
    • Check: The key signature of A-flat major has four flats (B-flat, E-flat, A-flat, and D-flat); D has a flat.
  • Example 8.3.2C:
    • The bottom note does not have an accidental and the interval number is 5.
    • The notes are not B and F.
    • Therefore, the top note also does not have an accidental.
    • Check: The key signature of F major has one flat (B-flat); C does not have a flat.
  • Example 8.3.2D:
    • The bottom note has a sharp and the interval number is 5.
    • The notes are not B and F.
    • Therefore, the top note also has a sharp.
    • Check: The key signature of F-sharp major has six sharps (F-sharp, C-sharp, G-sharp, D-sharp, A-sharp, and E-sharp); C has a sharp.

The reason why this shortcut works is because if you write out all fifteen major scales and all fifteen minor scales, the perfect fourth and the perfect fifth will always share the same accidental with the tonic except for F and B or B and F. What happens with these pairs of notes?

Example 8.3.3. F and B (or B and F)

Example A, F to B-flat is a perfect fourth. Example B, F-sharp to B is a perfect fourth. Example C, B to F-sharp is a perfect fifth. Example D, B-flat to F is a perfect fifth.

The accidentals for perfect fourths (between F and B) and perfect fifths (between B and F) will not match. You will need to rely on the key signatures for these intervals.

  • Example 8.3.3A:
    • The bottom note does not have an accidental and the interval number is 4.
    • The notes are F and B.
    • The key signature of F major has one flat (B-flat); therefore, B has a flat.
  • Example 8.3.3B:
    • The bottom note has a sharp and the interval number is 4.
    • The notes are F and B.
    • The key signature of F-sharp major has six sharps (F-sharp, C-sharp, G-sharp, D-sharp, A-sharp, and E-sharp); therefore, B does not have an accidental.
  • Example 8.3.3C:
    • The bottom note does not have an accidental and the interval number is 5.
    • The notes are B and F.
    • The key signature of B major has five sharps (F-sharp, C-sharp, G-sharp, D-sharp, and A-sharp); therefore, F has a sharp.
  • Example 8.3.3D:
    • The bottom note has a flat and the interval number is 5.
    • The notes are B and F.
    • The key signature of B-flat major has two flats (B-flat and E-flat); therefore, F does not have a flat.

It is simple to memorize which notes have an accidental when the notes are F and B.

  • If there is one sharp in the key signature, that sharp is F-sharp.
  • If there is one flat in the key signature, that flat is B-flat.
  • This means that if you see F and B, or B and F, the pair will have either F-sharp or B-flat.
    • F-sharp and B
    • F and B-flat
    • B and F-sharp
    • B-flat and F

This shortcut can help you quickly identify perfect intervals. In Example 8.3.4, Bosmans utilizes harmonic perfect intervals.

Example 8.3.4. Harmonic perfect intervals in Bosmans[9], Impressions for Cello and Piano, I. Cortége

Several intervals are pointed out in Busman's Impressions for Cello and Piano.

  • Example 8.3.4A: The interval between G and C is a fourth. Since the notes are not F and B and both notes do not have accidentals, this is a perfect fourth.
  • Example 8.3.4B: The interval between F and B-flat is a fourth. Because the notes are F and B, one note must have an accidental (B-flat). Therefore, this interval is also a perfect fourth.
  • Example 8.3.4C: The interval between E-flat and A-flat is a fourth. Since the notes are not F and B and the accidentals match, this is a perfect fourth.
  • Example 8.3.4D: The interval between D and G is a fourth. Since the notes are not F and B and both notes do not have accidentals, this is a perfect fourth.
  • Example 8.3.4E: The interval between G and G is an octave. Because both notes have no accidentals, this is a perfect octave.

Notice that in the explanations above, we did not relate every dyad to the key of the bottom note. Using the shortcut allowed us to identify the intervals more quickly.

Shortcut: P4/P5

A fast way to identify and write perfect fourths and perfect fifths is to remember that they use the same accidentals unless the notes are F and B, or B and F.

  • P4: F and B-flat
  • P4: F-sharp and B
  • P5: B-flat and F
  • P5: B and F-sharp

Practice 8.3A

Directions:

  • Identify the interval as quickly as possible. If the interval is not a P4 or P5, write an “X.”

Number 1, G-flat to D-flat. Number 2, F to B-sharp. Number 3, C-sharp to F-sharp. Number 4, D-flat to A. Number 5, B to F-sharp. Number 6, G-sharp to D-sharp. Number 7, F to B-flat. Number 8, B-flat to E. Number 9, D-sharp to A-sharp. Number 10, B-flat to F-flat. Number 11, A to D.

Click here to watch the tutorial.

Solution
1) P5
2) X
3) P4
4) X
5) P5
6) P5
7) P4
8) X
9) P5
10) X
11) P4

Practice 8.3B

Directions:

  • Write melodic intervals above the given note using half notes.

Number 1, a perfect fifth above B-flat. Number 2, a perfect fifth above G-sharp. Number 3, a perfect fourth above A-flat. Number 4, a perfect fourth above B. Number 5, a perfect fourth above D. Number 6, a perfect fifth above C-sharp. Number 7, a perfect fourth above F-sharp. Number 8, a perfect fifth above E-flat. Number 9, a perfect fourth above F. Number 10, a perfect fifth above D-flat. Number 11, a perfect fourth above G-flat. Number 12, a perfect fourth above E. Number 13, a perfect fourth above A-sharp. Number 14, a perfect fifth above B.

Click here to watch the tutorial.

Practice 8.3C

Directions:

  • Using the shortcut we learned, identify and label the fifths as quickly as possible.

Scriabin[10], Etude, Op. 65, No. 3

Score from Scriabin's Etude Op. 65, No. 3

Click here to watch the tutorial.

8.4  MINOR INTERVALS

When we take a major interval and reduce it by a half step (while maintaining its interval number), the quality of the interval becomes a minor interval (m). Perfect intervals can never become minor; only major intervals can become minor. In other words, only the second, third, sixth and seventh can be minor intervals: minor second, minor third, minor sixth and minor seventh.

There are two strategies you can use to quickly identify and write minor intervals: 1) starting from major intervals or 2) starting from the minor scale.

From the Major Intervals

We learned that in order to transform a major scale into its parallel natural minor scale, we lower [latex]\hat3[/latex], [latex]\hat6[/latex], and [latex]\hat7[/latex]. When we do this, we are also transforming the major third, major sixth, and major seventh to a minor third, minor sixth, and minor seventh. We would simply apply the same procedure to the major second to transform it to a minor second: lower it a half step.

When using this method, you must remember that you can never change the bottom note. You can only add an accidental to the top note.

Let’s practice writing a few minor intervals starting from the major intervals.

Step one: Write in the pitch that is found in the major scale.

Example 8.4.1. Step one

Example A, B to C-sharp is a major second. Example B, C to E is a major third. Example C, A-flat to F is a major sixth. Example D, C-flat to B-flat is a major seventh.

  • Example 8.4.1A: Because the key signature of B major has five sharps, a major second (M2) above B is C-sharp.
  • Example 8.4.1B: Because the key signature of C major has no sharps or flats, a major third (M3) above C is E.
  • Example 8.4.1C: Because the key signature of A-flat major has four flats, a major sixth (M6) above A-flat is F.
  • Example 8.4.1D: Because the key signature of C-flat major has all seven flats, a major seventh (M7) above C-flat is B-flat.

Step two: Lower the top note by a half step by adding, changing, or removing an accidental. Do not change the note (letter) name and do not adjust the bottom note.

Example 8.4.2. Step two

Example A lowered C# to C. Example B lowered E to E-flat. Example C lowered F to F-flat. Example D lowered B-flat to B-double-flat.

  • Example 8.4.2A: To change the major second to a minor second (m2), lower the C-sharp to C-natural. The natural sign is not necessary; simply remove the sharp.
  • Example 8.4.2B: To change the major third to a minor third (m3), lower the E to E-flat.
  • Example 8.4.2C: To change the major sixth to a minor sixth (m6), lower the F to F-flat.
    • Although E and F-flat are enharmonically equivalent, A to E would be a fifth and not a sixth. The top note must be written as F-flat.
  • Example 8.4.2D: To change the major seventh to a minor seventh (m7), lower the B-flat to B-double flat.
    • As in Example 8.4.2C, you must write B-double flat and not A. A is only a sixth above C and the directions ask for a minor seventh above C, so the answer must be B-something.

Notice that the top note can vary from no accidental, to a flat, to a double flat. Indeed, as we will later learn, you can even have minor intervals with a sharp or double sharp on the top note. In other words, there is no consistently reliable way to write a minor interval. Sometimes students will simply add a flat to the top note, but that is not always the case.

There is a famous example of lowering the top note of a major interval to become a minor interval in Strauss’s Also sprach Zarathustra (Example 8.4.3).

Example 8.4.3. Major to minor interval: Strauss[11], Also sprach Zarathustra (Thus Spoke Zarathustra), Op. 30 (Orchestral reduction)

Excerpt from Strauss, Also sprach Zarathustra shows a major third becoming a minor third.

In Example 8.4.3, the first bracket shows a major third (M3) from C to E. Across the bar line, the top note E is lowered to E-flat, creating a minor third (m3). Listen to the distinct qualities of the major third and the minor third.

Minor Intervals from Major Intervals

Write the major interval based on the major key signature, then lower the top note by adding, changing, or removing an accidental.

Practice 8.4A

Directions:

  • Using half notes, write melodic minor intervals above the given note by first writing the major interval, then lowering the top note a half step.

Number 1, minor third above F. Number 2, minor sixth above E-flat. Number 3, minor seventh above A. Number 4, minor sixth above F-sharp. Number 5, minor second above B-flat.

Click here to watch the tutorial.

From the Minor Key Signature

Another method you can use to find minor intervals is to base it off the natural minor scale. However, if you use this technique, you cannot apply it to minor seconds, as the second in the natural minor scale is a major second. Example 8.4.4. shows the minor intervals found in the natural minor scale.

Example 8.4.4. Intervals in the natural minor scale

The intervals in a natural minor scale are the perfect unison, major second, minor third, perfect fourth, perfect fifth, minor sixth, minor seventh and perfect octave. The minor third, sixth, and seventh are boxed because they are the minor intervals found in the minor scale.

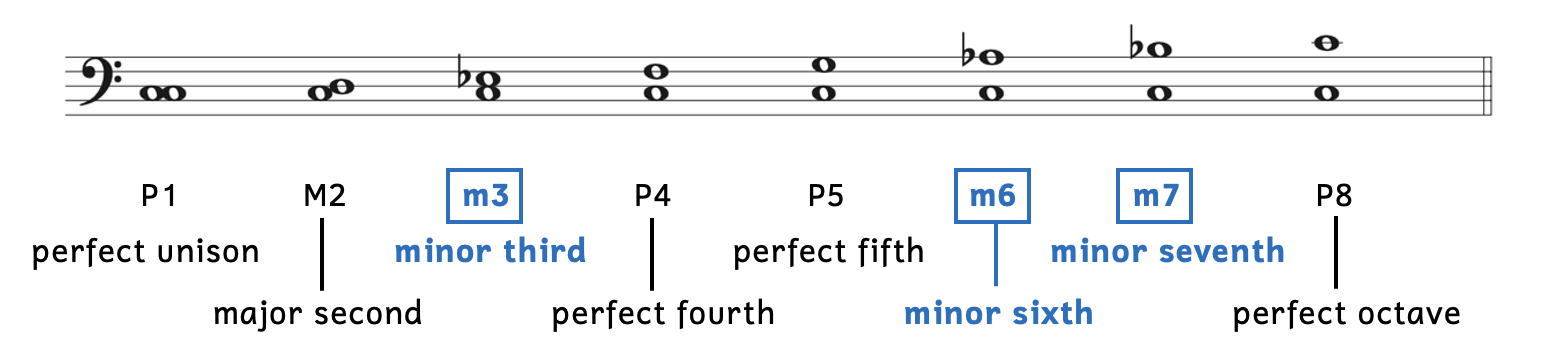
The first row shows how we label the interval and the bottom two rows show how we say the intervals.

  • Notice that the intervals in blue boxes (third, sixth, and seventh) are minor (m).
  • All the other intervals are exactly the same as in the major scale.
    • The perfect intervals are the same in major and minor. This is why the shortcut for perfect intervals works.
    • The second is major, not minor.

Some students prefer the minor key signature method because it only requires one step to find the minor intervals. Using the major key signature requires two steps: finding the major interval then lowering the top note with an accidental. However other students struggle with minor key signatures, so they prefer beginning with the major key signature.

Example 8.4.5. Minor intervals

Example A shows A-flat to C-flat is a minor third. Example B shows F-sharp to D is a minor sixth. Example C shows B-flat up to A-flat is a minor seventh.

  • Example 8.4.5A: The key signature of A-flat minor has all seven flats. Therefore, a minor third (m3) above A-flat is C-flat.
  • Example 8.4.5B: The key signature of F-sharp minor has three sharps (F-sharp, C-sharp, and G-sharp). Therefore, a minor sixth (m6) above F-sharp is D.
  • Example 8.4.5C: The key signature of B-flat minor has five flats (B-flat, E-flat, A-flat, D-flat, and G-flat). Therefore, a minor seventh (m7) above B-flat is A-flat.

All the notes and intervals in Example 8.4.6 belong to the key of A minor excerpt for one (marked with an asterisk).

Example 8.4.6. Intervals in Beach, Theme and Variations for Flute and String Quartet, Op. 80 – Theme. Lento di molto, sempre espressivo

Numerous intervals are shown in Beach's Theme and Variations for Flute and String Quartet, Op. 80

  • Remember that intervals are always based on the lowest note. In Example 8.4.6, the cello has the lowest note, A3.
    • Because the other instruments (violin I, violin, II, and viola) are higher than the cello, the intervals are based on the cello’s A3.
    • Since the key is A minor and A is the lowest note, all the intervals listed (except the one with an asterisk) belong to the A minor scale.
  • The intervals between the viola and cello, and the intervals between the second violin and the cello are shown. The intervals between the first violin and the cello are not shown because the distance is greater than an octave. Intervals greater than an octave will be covered in Chapter 9 (More Intervals).
  • The last interval between the viola and cello (with an asterisk) does not belong to the minor scale. However, we can use the minor key signature to help us find major intervals.
    • The penultimate interval between the viola and bass is a minor third, since C belongs to the key of A minor.
    • The next pitch in the viola is C-sharp, which does not belong to the key of A minor. By raising C to C-sharp, the interval becomes larger—therefore changing the interval from a minor third to a major third.

Alternatively, you could have used the key signature of the parallel major to get to the answer of a major third.

What happens when you try to find the parallel major of a key that does not exist? As you may recall, there are three minor keys that do not have a parallel major: G-sharp minor, D-sharp minor, and A-sharp minor. When writing major intervals above G-sharp, D-sharp, or A-sharp, use the minor key signature, then raise the top note.

Example 8.4.7. Major intervals from the minor key signature

Example A shows a major third above G-sharp is B-sharp. Example B shows a major sixth above D-sharp is B-sharp. Example C shows a major seventh above A-sharp is G-double sharp.

  • Example 8.4.7A: There is no such key signature of G-sharp major, but G-sharp minor has five sharps. Therefore, a minor third above G-sharp is B. Raising B to B-sharp results in a major third (M3).
  • Example 8.4.7B: There is no such key signature of D-sharp major, but D-sharp minor has six sharps. Therefore, a minor sixth above D-sharp is B. Raising B to B-sharp results in a major sixth (M6).
  • Example 8.4.7C: There is no such key signature of A-sharp major, but A-sharp minor has all seven sharps. Therefore, a minor seventh above A-sharp is G-sharp. Raising G-sharp to G-double sharp results in a major seventh (M7).

It is best to know both techniques. For notes above G-sharp, D-sharp, or A-sharp, it is easiest to start with the minor key signature. On the other hand, there are three major keys that do not have a parallel minor: D-flat major, G-flat major, and C-flat major. When writing minor intervals above D-flat, G-flat, or C-flat, basing it off the major interval would be easier. In the next section, we will learn how to deal with other trickier intervals.

Minor Intervals from Minor Keys

In the natural minor scale, 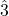[latex]\hat3[/latex] is a minor third, 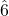[latex]\hat6[/latex] is a minor sixth, and 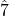[latex]\hat7[/latex] is a minor seventh. Use the minor key signature to identify those minor intervals. For minor seconds, you must still lower the top note a half step because 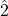[latex]\hat2[/latex] in minor scales is a major second.

Practice 8.4B

Directions:

  • Using half notes, write the minor intervals above the given note by using the minor key signature.

Number 1, minor sixth above A-sharp. Number 2, minor third above D-sharp. Number 3, minor seventh above F. Minor 4, minor third above G-sharp. Number 5, minor sixth above B-flat.

Click here to watch the tutorial.

Practice 8.4C

Directions:

  • Using half notes, write melodic minor intervals above the given note by using either method.

Number 1, minor seventh above F-sharp. Number 2, minor second above E. Number 3, minor third above A-sharp. Number 4, minor sixth above D-flat. Number 5, minor third above G-sharp. Number 6, minor second above C-flat. Number 7, minor seventh above A. Number 8, minor sixth above D-sharp. Number 9, minor sixth above G-flat. Number 10, minor third above B. Number 11, minor sixth above B. Number 12, minor third above C-sharp. Number 13, minor seventh above G. Number 14, minor second above F-sharp. Number 15, minor seventh above G-sharp.

Click here to watch the tutorial.

Practice 8.4D

Directions:

  • Identify the interval. The interval can be minor, major, or perfect.

Number 1, F-sharp to A-sharp. Number 2, B to C. Number 3, E-flat to B-flat. Number 4, G to F-sharp. Number 5, C-sharp to E. Number 6, A-flat up to A-flat. Number 7, D-sharp up to C-sharp. Number 8, B up to E. Number 9, G-flat up to E-flat. Number 10, F up to A-flat. Number 11, E up to F. Number 12, C-flat up to G-flat. Number 13, B-flat up to G-flat. Number 14, G-sharp up to B-sharp. Number 15, C up to B-flat. Number 16, A up to B. Number 17, D-flat up to F-flat.

Click here to watch the tutorial.

Solution
1) M3
2) m2
3) P5
4) M7
5) m3
6) P8
7) m7
8) P4
9) M6
10) m3
11) m2
12) P5
13) m6
14) M3
15) m7
16) M2
17) m3

Practice 8.4E

Directions:

  • Identify all the intervals between the bass and upper voices. In this case, the “bass” is Alto #2 and the upper voices are Soprano #1, Soprano #2, and Alto #1. Write the intervals between Soprano #1 and Alto #2; Soprano #2 and Alto #2; and Alto #1 and Alto #2. See Practice 8.2C for a sample.

Reichardt, “Weihnachten: Welche Morgenröten wallen”

Identify intervals in Reichardt, Weihnachten Morgenröten wallen

Click here to watch the tutorial.

Solution
1) m7
2) M6
3) P5
4) M6
5) P8
6) M6
7) P4
8) m3
9) M3
10) m3

8.5  SHORTCUT: m2/M2

As we learned, the minor second is not found in the natural minor scale. For this reason, we could not use the minor key signature to find the minor second. We could use the first method—beginning with a major second then lowering the top note by a half step—but there is a faster shortcut.

  • A minor second is a diatonic half step.

Always write the second first, because a chromatic half step would be incorrect. Example 8.5.1 shows a variety of minor seconds.

Example 8.5.1. Minor seconds

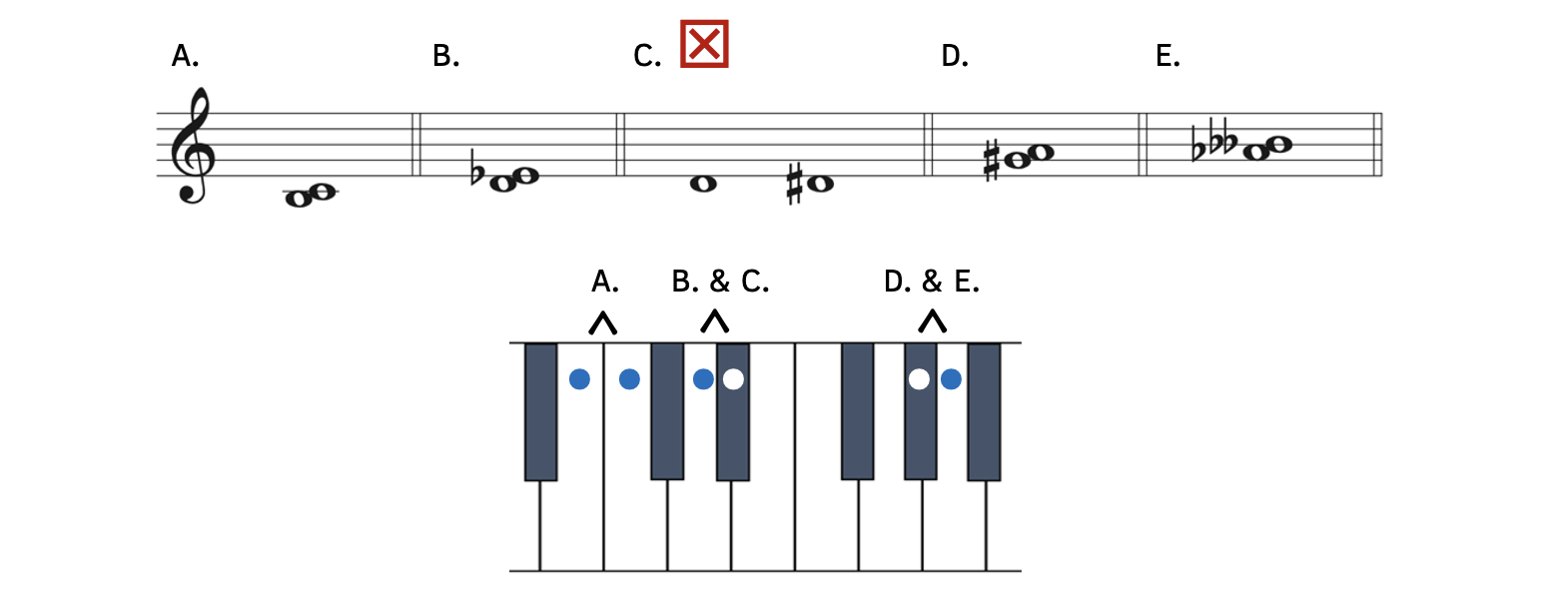
Example A is a half step and minor second from E to F. Example B is a half step and minor second from F to G-flat. Example C is a half step but not a minor second from D to D-sharp. Example D is a half step and minor second from G-sharp to A. Example E is a half step and minor second from A-flat to B-double flat.

For each of the examples above, you could think of the major key or minor key, then lower the second by a half step, but it is much quicker to simply think of a diatonic half step above.

  • Example 8.5.1A: B to C is a half step and a minor second, as shown on the keyboard.
  • Example 8.5.1B: D to E-flat is also a half step and a minor second, as shown on the keyboard.
  • Example 8.5.1C: D to D-sharp is a half step, but is not a minor second. D to D-sharp is a type of unison, so although it is a half step, it is not a minor second.
  • Example 8.5.1D: G-sharp to A is a half step and a minor second, as shown on the keyboard.
  • Example 8.5.1E: A-flat and B-double flat is a half step and a minor second, as shown on the keyboard. To identify this interval, simply locate the pitches on the keyboard. If the notes form a second and are a half step apart, the interval is a minor second.

You can also use a similar method to quickly identify and write major seconds.

  • A major second is a diatonic whole step.

Again, always write the second first. Example 8.5.2 shows a variety of major seconds.

Example 8.5.2. Major seconds

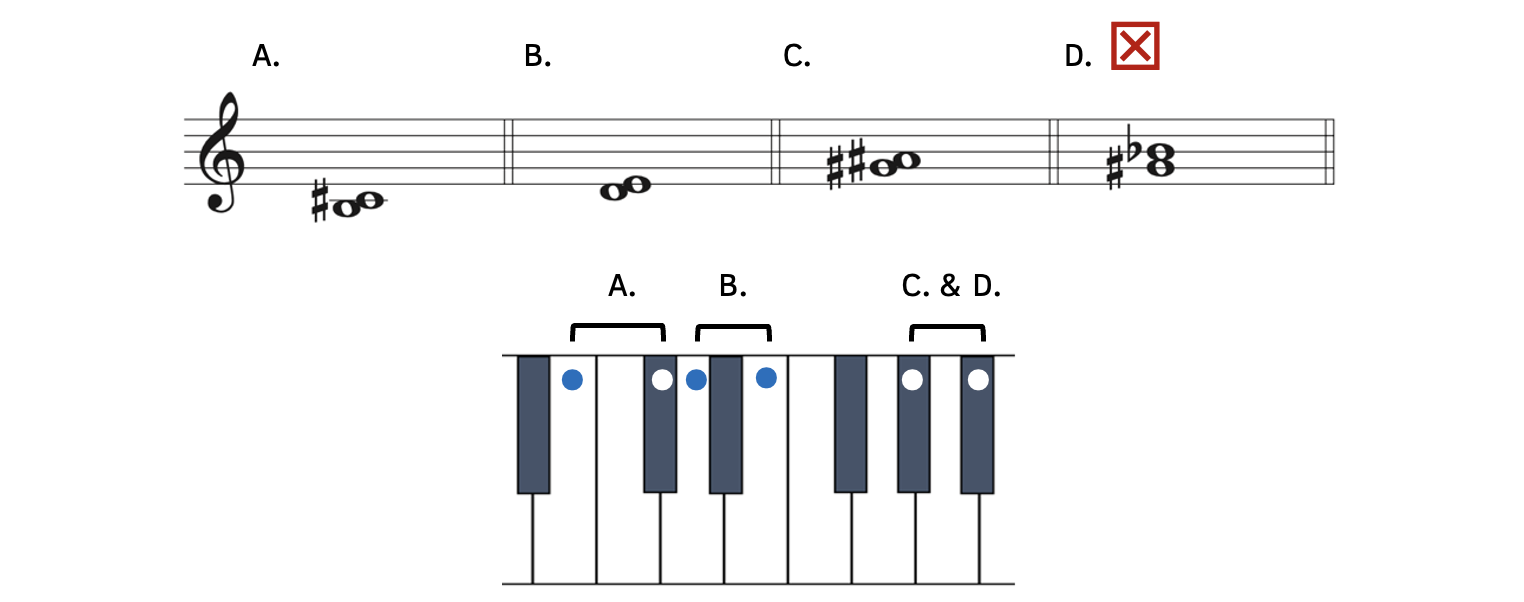
Example A is from B to C-sharp and it is a major second. Example B is from D to E and it is a major second. Example C is from G-sharp to A-sharp and it is a major second. Example D is from G-sharp to B-flat. Although its placement on the keyboard is the same as Example C, it is not a major second because the note names are a third apart.

For each of the examples above, you could think of [latex]\hat2[/latex] in the major key or minor key, but it is sometimes faster to simply think of a diatonic half step above.

  • Example 8.5.2A: B to C-sharp is a whole step and a major second, as shown on the keyboard.
  • Example 8.5.2B: D to E is also a whole step and a major second, as shown on the keyboard.
  • Example 8.5.2C: G-sharp to A-sharp is a whole step and a major second, as shown on the keyboard.
  • Example 8.5.2D: G-sharp to B-flat is a whole step, but is not a major second. G to B is a third, so although it is a whole step, it is not a major second.

In Chapter 4, we learned that a major scale was made from a pattern of whole steps (W) and half steps (H): WWHWWWH. We can now change these half steps and whole steps to minor seconds and major seconds.

Example 8.5.3. Steps in a major scale

The steps in a major scale are whole whole half, whole whole whole half. Whole steps are major seconds and half steps are minor seconds.

Using diatonic half steps (m2) and diatonic whole steps (M2), see if you can quickly identify the seconds in Example 8.5.4.

Example 8.5.4. Seconds in Farrenc[12], Impromptu pour Piano

There are a number of minor seconds and major seconds in Farrenc's Impromptu pour Piano. The last interval is not a second, as the notes are E and E-sharp.

  • For the notes with stems pointing up, the intervals are all minor seconds and major seconds.
    • If you base the interval of the first two notes on the key signature of the lower note (E-sharp), it would be extremely difficult to figure out if the interval from E-sharp to F-sharp is a minor second or major second. However, the distance between E-sharp and F-sharp is a diatonic half step. Therefore, the interval is a minor second (m2).
  • For the notes with the stems pointing down, the intervals are all minor and major seconds except for the last interval.
    • Although E-natural to E-sharp is a half-step apart, it is a chromatic half step (same letter name). Therefore, this interval is a type of unison, and not a second.

Shortcut: m2/M2

  • Minor seconds (m2) are diatonic half steps.
  • Major seconds (M2) are diatonic whole steps.

Practice 8.5A

Directions:

  • Identify the interval as quickly as possibly. If the interval is not a m2 or M2, write an “X.”

Number 1, A to B. Number 2, A to B-flat. Number 3, A-sharp to B. Number 4, A-flat to B. Number 5, A-flat to B-double flat. Number 6, B to C-sharp. Number 7, B-flat to C-sharp. Number 8, B to C. Number 9, B-flat to C-flat. Number 10, B-flat to C. Number 11, B to C-flat. Number 12, C-flat to D-flat. Number 13, C to D-flat. Number 14, C-sharp to D-sharp. Number 15, C to D-double flat. Number 16, D-flat to D-double flat. Number 17, C-double sharp to D-sharp.

Click here to watch the tutorial.

Solution
1) M2
2) m2
3) m2
4) X
5) m2
6) M2
7) X
8) m2
9) m2
10) M2
11) X
12) M2
13) m2
14) M2
15) X
16) m2
17) m2

Practice 8.5B

Directions:

  • Write the melodic interval above the given note using half notes.

Number 1, Minor second above A-sharp. Number 2, major second above A-flat. Number 3, major second above G-sharp. Number 4, minor second above B-flat. Number 5, minor second above E-sharp. Number 6, major second above F-flat. Number 7, minor second above C-flat. Number 8, minor second above B-sharp. Number 9, major second above D-sharp. Number 10, major second above C. Number 11, minor second above F. Number 12, major second above G-flat. Number 13, major second above F-sharp. Number 14, minor second above B.

Click here to watch the tutorial.

Practice 8.5C

Directions:

  • Identify and label all the minor seconds and major seconds in the flute part.

Boulanger[13], Nocturne for Flute or Violin and Piano

Score to Boulanger's Nocturne for Flute and Piano

Click here to watch the tutorial.

8.6  TRICKY INTERVALS

We just learned how to write minor and major seconds starting on all notes—including those that do not have a key signature, such as E-sharp. We will now learn how to identify and write other intervals that begin on tricky notes.

We learned that not all notes have both major and minor keys.

Example 8.6.1. Possible key signatures in major and/or minor

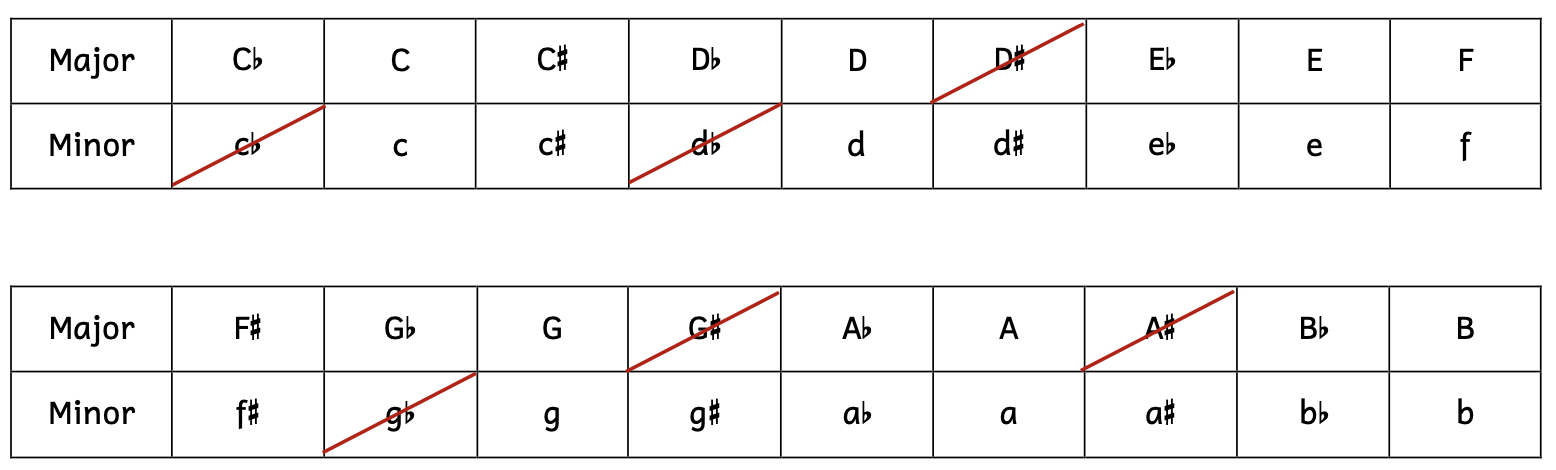
Chart showing that not all key signatures are possible. D-sharp, G-sharp, and A-sharp are not possible, while C-flat, D-flat, and G-flat are not possible.

  • For notes that have keys in both major and minor, such as C major and C minor, you can choose which technique to use to create and identify intervals. For example, to write a minor sixth above C, you have two choices:
    • Think of the key signature of C major. Write a major sixth above C, then lower the top note a half step by using an accidental.
    • Think of the key signature of C minor. Write a minor sixth above C based on the key signature of C minor.
  • For notes that have keys only in major, such as D-flat major, think of the key signature of D-flat major and lower the top note for minor intervals.
  • For notes that have keys only in minor, such as D-sharp minor, think of the key signature of D-sharp minor and raise the top note for major intervals.

However, what happens when a note does not have a major or minor key? For example, what is a major sixth above F-flat? There is no such key as F-flat major or F-flat minor. Although not as common, we do encounter tricky intervals like this.

Identifying Tricky Intervals

When tricky intervals share the same accidentals, you can cross out both accidentals because the quality will remain the same.

Example 8.6.2. Simplifying tricky intervals with the same accidentals

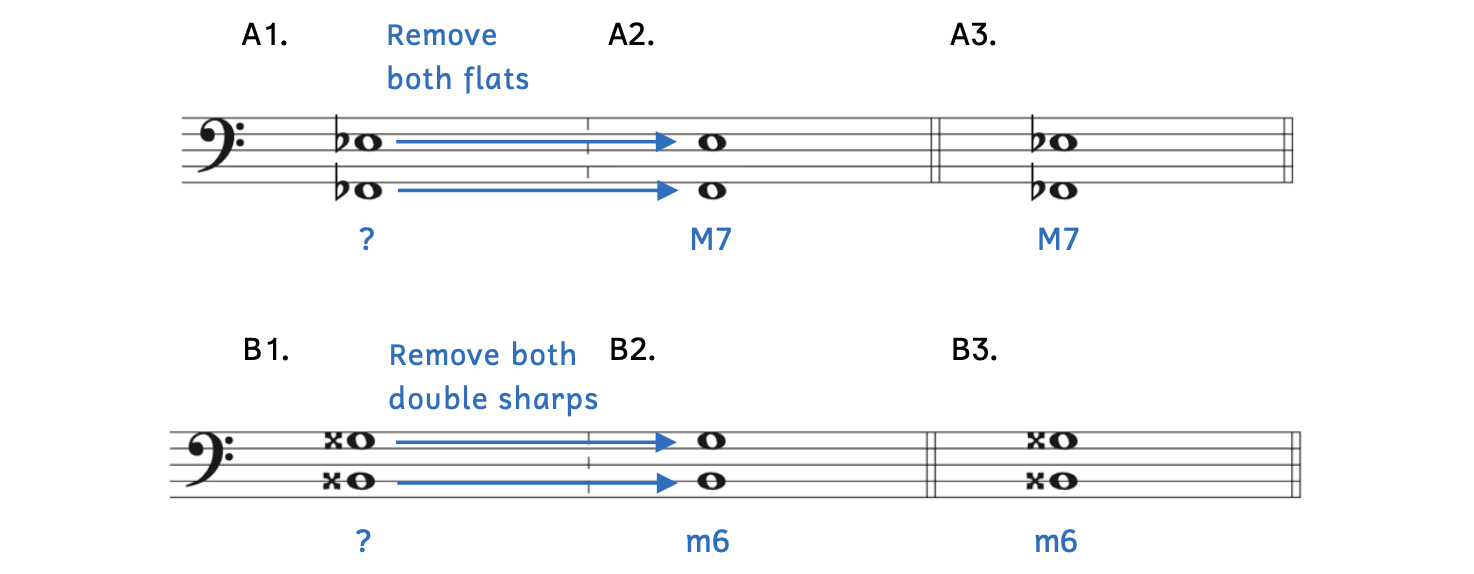
Example A1 shows F-flat up to E-flat. Example A2 removes both flats to find the answer, a major seventh. Example B1 shows B-double-sharp up to G double-sharp. Example B2 removes both sharps to find the answer, a minor sixth.

  • Example 8.6.2A:
    • A1: The bottom note of the interval is F-flat, which appears daunting.
    • A2: Because both accidentals match (they are both flats), simply remove both flats to easily figure out the interval. The interval from F to E is a major seventh (M7).
    • A3: Returning back to the original notes (F-flat and E-flat), we transfer our answer, M7.
  • Example 8.6.2B:
    • B1: The bottom note of the interval is B-double sharp, which looks intimidating.
    • B2: Because both accidentals match (they are both double sharps), simply remove both double sharps to easily figure out the interval. The interval from B up to G is a minor sixth (m6).
    • B3: Returning back to the original notes (B-double sharp and G-double sharp), we transfer our answer, m6.
    • Notice that although the interval was smaller than a seventh, the double sharps are aligned. This is because double sharps are smaller accidentals that do not overlap in this example.

To identify tricky intervals where the accidentals do not match, follow these steps.

Step one: Change the accidental of the bottom note to a natural sign and make the same type of change to the top note. You can only change the notes by using accidentals: you cannot change the note names.

  • If you raise a flatted bottom note to a natural, then raise the top note a half step.
  • If you lower a sharped bottom note to a natural, then lower the top note a half step.

Step two: Apply the same steps you usually would to identify intervals, then write your answer for the original interval.

Example 8.6.3. Simplifying tricky intervals with different accidentals

Example A1 shows F-flat up to D-double flat. Example A2 raises F-flat by a half step to F. Example A2 applies the same change to the top note: D-double flat is raised by a half step to D-flat. The resulting interval is F up to D-flat, which is a minor sixth. Example B1 shows B-sharp up to F-double sharp. Example B2 lowers the B-sharp by a half step to B-natural. Example B2 applies the same change to the top note: F-double sharp down to F-sharp. 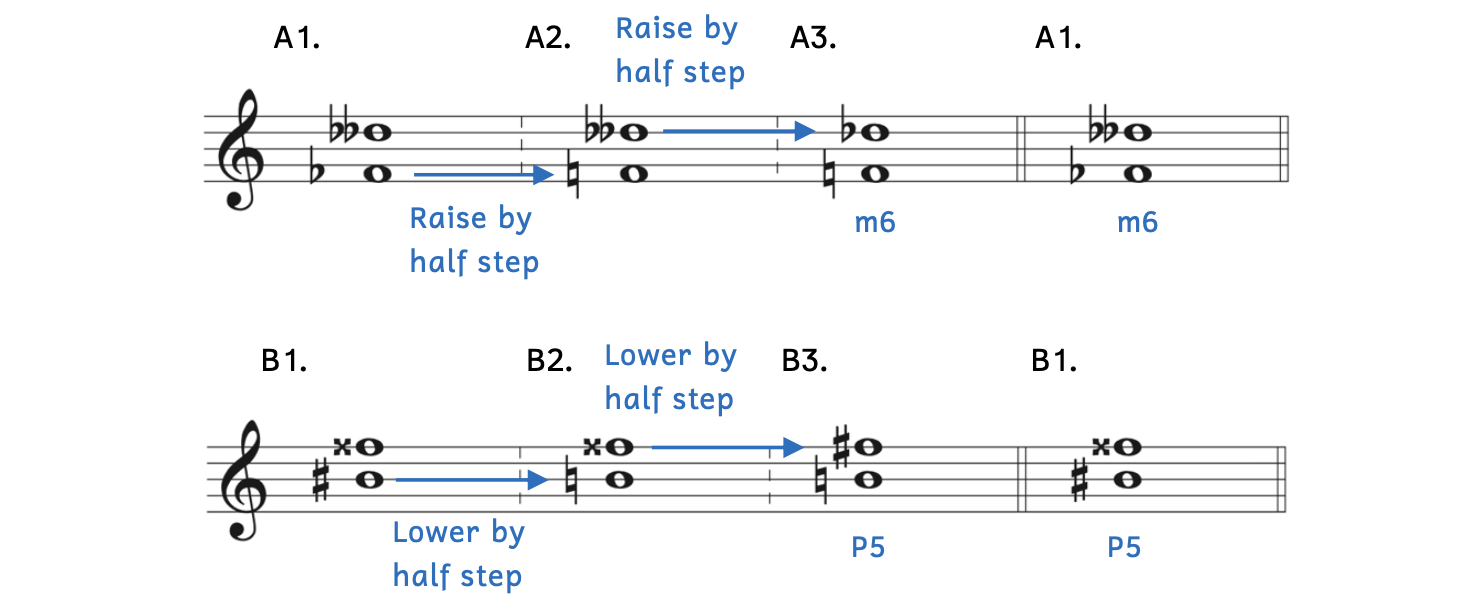The resulting interval is B to F-sharp, which is a perfect fifth.

  • Example 8.6.3A: There is no such key as F-flat major or F-flat minor.
    • A1 to A2: Raise F-flat a half step to become F-natural.
    • A2 to A3: Apply the same transformation to the top note: Raise the top note (D-double flat) by a half step to D-flat.
    • A3: The interval from F to D-flat is manageable; it is a minor sixth (m6).
    • A1: Returning back to the original notes (F-flat and D-double flat), transfer your answer: m6.
  • Example 8.6.3B: There is no such key as B-sharp major or B-sharp minor.
    • B1 to B2: Lower B-sharp a half step to become B-natural.
    • B2 to B3: Apply the same transformation to the top note: Lower the top note (F-double sharp) by a half step to F-sharp.
    • B3: The interval from B to F-sharp is manageable; it is a perfect fifth (P5).
    • B1: Returning back to the original notes (B-sharp to F-double sharp), transfer your answer: P5.
    • Alternatively, we could use the shortcut for perfect fifths to quickly identify this interval.

We can use this technique for even more extreme bottom notes, including double flats and double sharps. Apply the same steps, but instead of adjusting notes by a half step, adjust them by a whole step.

Example 8.6.4. Extreme bottom notes

Example A1 shows E-double flat up to G-flat. Example A2 shows E-double flat raised by a whole step to E-natural. Example A3 shows the same change applied to the top note so G-flat is raised by a whole step to G-sharp. The interval is now E to G-sharp, which is a major third. Example B1 shows F-double sharp up to B-sharp. Example B2 shows F-double sharp raised by a whole step to F-natural. Example B3 shows the same change applied to the top note so B-sharp is lowered by a whole step to B-flat. 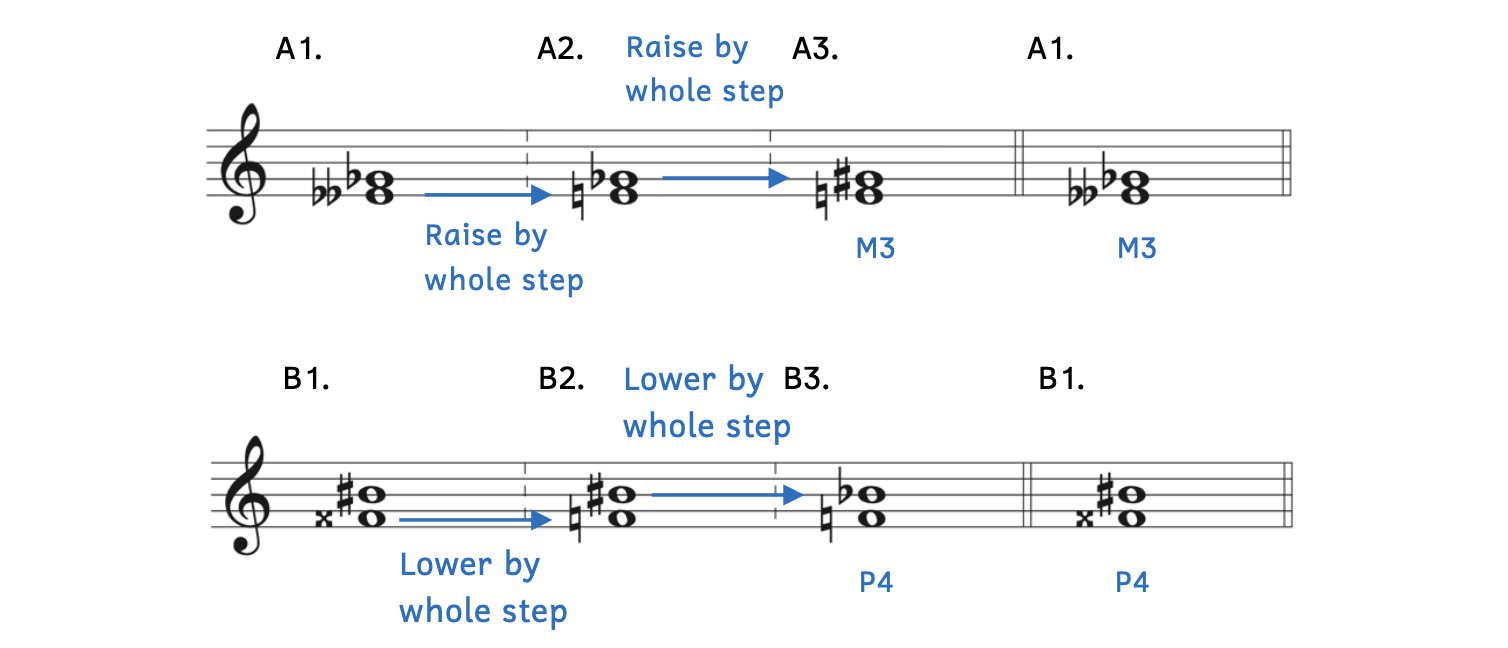The interval is now F to B-flat, which is a perfect fourth.

  • Example 8.6.4A:
    • A1 to A2: Raise E-double flat a whole step to become E-natural.
    • A2 to A3: Apply the same transformation to the top note: Raise the top note (G-flat) by a whole step to G-sharp. You cannot raise the top note to A-flat because E to A would be a fourth and the interval must be a third.
    • A3: The interval from E to G-sharp is manageable; it is a major third (M3).
    • A1: Returning back to the original notes (E-double flat to G-flat), we transfer our answer: M3.
  • Example 8.6.4B:
    • B1 to B2: F-double sharp must be lowered a whole step to become F-natural.
    • B2 to B3: Apply the same transformation to the top note: Lower the top note (B-sharp) by a whole step to B-flat. Again, you cannot lower the top note to A-sharp because F to A would be a third and the interval must be a fourth.
    • B3: The interval from F to B-flat is manageable; it is a perfect fourth (P4).
    • B1: Returning back to the original notes (F-double sharp to B-sharp), we transfer our answer, P4.
    • Alternatively, we could use the shortcut for perfect fourths to quickly identify this interval.

In Example 8.6.4, both bottom notes did not have to move by whole step; they could have been moved by only a half step.

  • Example 8.6.4A: Raising E-double flat by only a half step results in E-flat as the bottom note (instead of E-natural). In this case, you would only raise the top note a half step from G-flat to G-natural. The interval from E-flat to G is a major third (M3).
  • Example 8.6.4B: Lowering F-double sharp by only a half step results in F-sharp as the bottom note (instead of F-natural). In this case, you would only lower the top note a half step from B-sharp to B-natural. The interval from F-sharp to B is a perfect fourth (P4).

As you can see, whether you move the bottom note by a half step or a whole step, you get the same answer. Sometimes students prefer identifying intervals where the bottom note does not have an accidental. Other times, students prefer moving notes by only a half step rather than by a whole step. As usual, it is best to be able to apply both techniques.

Although you may wonder why we would need to learn about intervals with tricky bottom notes, they actually occur quite frequently in music. Example 8.6.5 shows an interval where the bottom note does not have a key.

Example 8.6.5. Tricky interval: Zybina[14], Mazurka

E-sharp up to C-sharp is circled in Zybina's Mazurka. The interval is a minor sixth.

In Example 8.6.5, the circled dyad is a tricky interval with E-sharp on the bottom.

  • There is no such key as E-sharp major or E-sharp minor.
  • Because the accidentals match, we can temporarily remove both sharps. Now the notes are E and C.
  • The key of E minor has one sharp (F-sharp). Therefore, E up to C is a minor sixth.
  • This means that the circled interval is also a minor sixth.

Identifying Intervals with Tricky Bottom Notes

Do not panic when the bottom note does not have a key signature. Simply change the bottom note temporarily to an existing key to make the answer easier to find. Be sure to apply the same change to the top note to identify the interval.

Writing Tricky Intervals

Writing intervals with tricky bottom notes requires similar steps as identifying them. Change the bottom note temporarily to a note that is easier for you.

Example 8.6.6. Writing tricky intervals

Example A1 asks for a major sixth above B-sharp. Example A2 shows that B-sharp is lowered by a half step to B. Example A3 shows a major sixth above B, which is G-sharp. Returning back to Example A1, B is raised by a half step to B-sharp and G-sharp is also raised by a half step to G-double sharp. Example B1 asks for a minor seventh above A-double flat. Example B2 shows that A-double flat is raised by a whole step to A-natural. Example B3 shows a minor seventh above A, which is G. Returning back to Example B1, A is lowered by a whole step to A-double flat and G is also lowered by a whole step to G-double flat.

  • Example 8.6.6A:
    • A1: Directions ask to write a major sixth (M6) above B-sharp.
    • A1 to A2: Because there is no such key as B-sharp major or B-sharp minor, temporarily lower B-sharp by a half step to B-natural.
    • A3: Write a major sixth above B: G-sharp.
    • A1: Return back to the original question. Since B-sharp is a half step higher than B, also raise G-sharp a half step to G-double sharp. Therefore, a major sixth above B-sharp is G-double sharp.
  • Example 8.6.6B:
    • B1: Directions ask to write a minor seventh (m7) above A-double flat.
    • B1 to B2: Because there is no such key as A-double flat major or A-double flat minor, temporarily raise A-double flat by a whole step to A-natural.
    • B3: Write a minor seventh above A: G.
    • B1: Return back to the original question. Since A-double flat is a whole step lower than A, also lower G a whole step to G-double flat. Therefore, a minor seventh above A-double flat is G-double flat.
    • Alternatively, instead of raising A-double flat a whole step to A, you could have raised A-double flat by a half step to A-flat. You would follow the same directions but apply a half step instead of a whole step.

Writing Intervals with Tricky Bottom Notes

  1. Temporarily change the bottom note to a note that has a key.
  2. Solve the interval.
  3. Returning to the original question, apply the same transposition to the top note as you did to the bottom note.

Practice 8.6A

Directions:

  • Identify the intervals. Use the empty staff as scratch paper.
    • You can use other shortcuts we have learned for perfect intervals and seconds.

Number 1, F-flat up to D-flat. Number 2, G-double sharp up to B-sharp. Number 3, B-sharp up to F-double sharp. Number 4, E-sharp up to A-sharp. Number 5, D-double flat up to E-double flat. Number 6, A-double sharp up to A double sharp. Number 7, B-sharp up to G0sharp. Number 8, B-double flat up to F-flat. Number 9, F-flat up to E-double flat. Number 10, D-double sharp to the same D-double sharp. Number 11, E-double flat up to G-flat.

Click here to watch the tutorial.
Solution
1) M6
2) m3
3) P5
4) P4
5) M2
6) P8
7) m6
8) P5
9) m7
10) P1
11) M3

 

Practice 8.6B

Directions:

  • Write melodic intervals above the given note using half notes. Use the empty staff as scratch paper.
    • You can use other shortcuts we have learned for perfect intervals and seconds.

Number 1, write a major third above B-sharp. Number 2, write a minor sixth above A-double flat. Number 3, write a minor second above E-sharp. Number 4, write a perfect fifth above D-double sharp. Number 5, write a minor third above F-flat. Number 6, write a major sixth above E-sharp. Number 7, write a perfect fourth above G-double sharp. Number 8, write a major second above C-double flat. Number 9, write a major third above E-double flat.

Click here to watch the tutorial.

Practice 8.6C

Directions:

  • Identify the circled intervals. Use the empty staff as scratch paper.

Carreño[15], Deux élégies, Op. 17, “Plainte!”

Number 1, B-sharp up to D-sharp are circled. Number 2, C-sharp up to E are circled. Number 3, A down to G-sharp are circled. Number 4, A-sharp up to B-sharp are circled. Number 5, G-sharp down to F-double sharp are circled. Number 6, G-sharp down to D-sharp are circled.

Click here to watch the tutorial.

Solution
1) m3
2) m3
3) m2
4) M2
5) m2
6) P4

8.7  SHORTCUT: m3/M3

Minor thirds and major thirds are particularly important in music. They are the building blocks for what we will be learning in future chapters. The ability to identify and write thirds quickly is extremely beneficial.

There is a special method you can use to quickly identify and write thirds. It involves memorizing the qualities of thirds based on white keys on the piano keyboard.

Major Thirds

Example 8.7.1 illustrates the C major scale with harmonic thirds written above each member of the scale.

Example 8.7.1. Thirds

C to E is a major third. D to F is a minor third. E to G is a minor third. F to A is a major third. G to B is a major third. A to C is a minor third. B to D is a minor third. The three major thirds from C, F, and G are boxed.

Notice that there are only three major thirds when you create thirds from the white keys on the piano keyboard: C/E, F/A, and G/B. These major thirds are shown by the blue boxes.

One way to remember these three major thirds is that in the key of C major, the perfect intervals are on C, F, and G (i.e., perfect unison/octave, perfect fourth and perfect fifth). Similarly, the major thirds begin on C, F, and G.

Because C/E, F/A, and G/B are major thirds, this means that if they have the same accidentals, they will also be major thirds.

Example 8.7.2. Major thirds

Example A, G to B is a major third. Example B, G-sharp to B-sharp is a major third. Example C, G-flat to B-flat is a major third. Example D, G-double sharp to B-double sharp is a major third. Example E, G-double flat to B-double flat is a major third.

Every third in Example 8.7.2 is a major third because the accidentals match. Because G/B is a major third, any combination of the same accidentals will also be a major third.

There are two ways to transform an interval to be a half step smaller: you can either lower the top note a half step, or raise the bottom note a half step. We can visualize these transformations on a keyboard.

Example 8.7.3. Transforming intervals on a keyboard

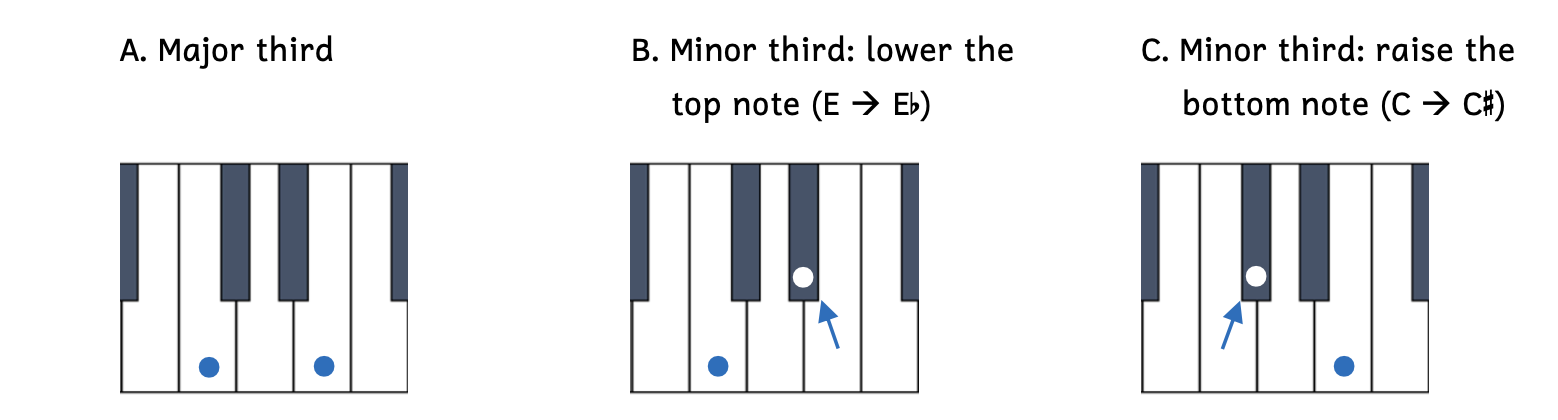
Example A shows a major third between C and E. Example B shows a minor third is created by lowering the top note E a half step to E-flat. Example C shows another way a minor third is created: by raising the bottom note C a half step to C-sharp.

  • Example 8.7.3A: C to E is an all-white-key major third.
  • Example 8.7.3B: C to E-flat is a minor third because the top note (E) has been lowered by a half step to E-flat.
  • Example 8.7.3C: C-sharp to E is also a minor third, but this time it is because the bottom note (C) has been raised by a half step to C-sharp.

Students usually grasp the concept of lowering the top note to make an interval smaller, but sometimes struggle with the idea that raising the bottom note also makes an interval smaller. They often associate sharps with making an interval larger. However, if the bottom is raised, the space becomes smaller.

Example 8.7.4. Making an interval smaller

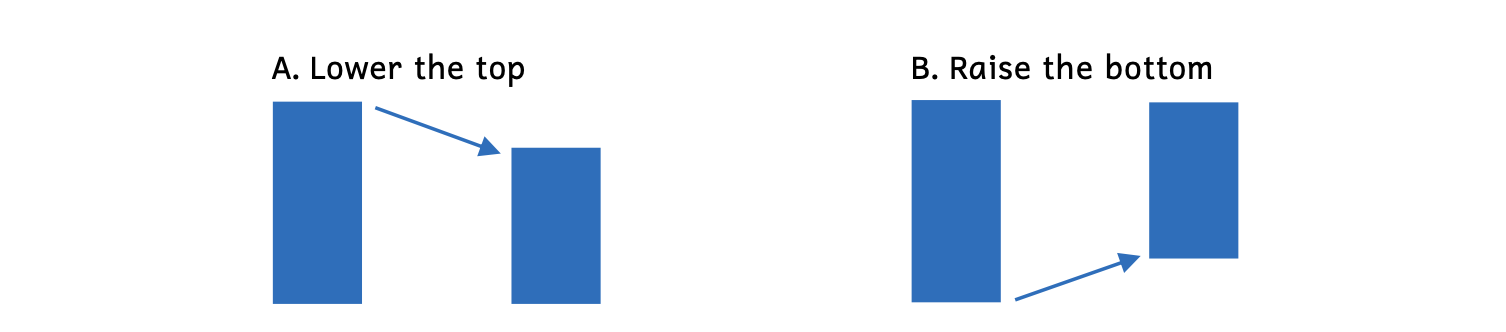
Example A shows making an interval smaller by lowering the top. Example B shows making an interval smaller by raising the bottom.

In Example 8.7.4, notice how the second rectangle in both examples is smaller.

  • Example 8.7.4A: Lowering the top makes the rectangle smaller.
  • Example 8.7.4B: Raising the bottom also makes the rectangle smaller.

In order to quickly transform major thirds on C, F, and G into minor thirds, we can lower the top note by a half step.

Example 8.7.5. Minor thirds by lowering the top note

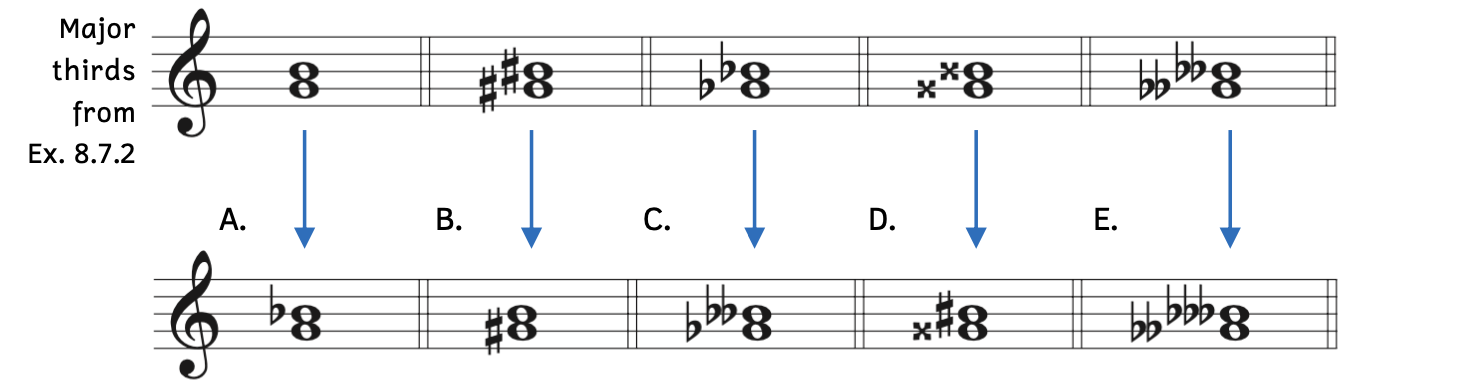
Example A shows lowering B to B-flat creates a minor third. Example B shows lowering B-sharp to B creates a minor third. Example C shows lowering B-flat to B-double flat creates a minor third. Example D shows lowering B-double sharp to B-sharp creates a minor third. Example E shows lowering B-double flat to B-triple flat creates a minor third.

  • Example 8.7.5A: Because G/B is a major third, lowering the top note from B to B-flat makes the interval a minor third.
  • Example 8.7.5B: Because G-sharp/B-sharp is a major third, lowering the top note from B-sharp to B makes the interval a minor third.
  • Example 8.7.5C: Because G-flat/B-flat is a major third, lowering the top note from B-flat to B-double flat makes the interval a minor third.
  • Example 8.7.5D: Because G-double sharp/B-double sharp is a major third, lowering the top note from B-double sharp to B-sharp makes the interval a minor third.
  • Example 8.7.5E: Because G-double flat/B-double flat is a major third, lowering the top note from B-double flat to B-triple-flat makes the interval a minor third.
    • When you lower a double flat a half step, it becomes a triple flat. Triple flats are rarely encountered except in abstract theory exercises.

We can also transform major thirds on C, F, and G into minor thirds by raising the bottom note by a half step.

Example 8.7.6. Minor thirds by raising the bottom note

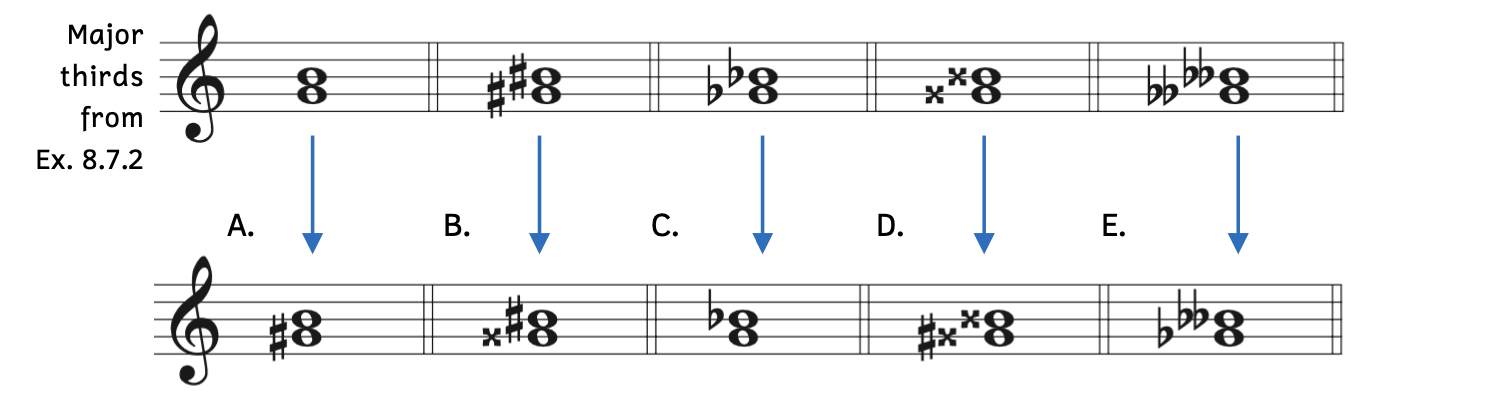
Example A shows that raising the bottom note G to G-sharp creates a minor third. Example B shows that raising the bottom note G-sharp to G-double sharp creates a minor third. Example C shows that raising the bottom note G-flat to G creates a minor third. Example D shows that raising the bottom note G-double sharp to G-triple sharp creates a minor third. Example E shows that raising the bottom note G-double flat to G-flat creates a minor third.

  • Example 8.7.6A: Because G/B is a major third, raising the bottom note from G to G-sharp makes the interval a minor third.
  • Example 8.7.6B: Because G-sharp/B-sharp is a major third, raising the bottom note from G-sharp to G-double sharp makes the interval a minor third.
  • Example 8.7.6C: Because G-flat/B-flat is a major third, raising the bottom note from G-flat to G makes the interval a minor third.
  • Example 8.7.6D: Because G-double sharp/B-double sharp is a major third, raising the bottom note from G-double sharp to G-triple sharp makes the interval a minor third.
      • When you raise a double sharp a half step, it becomes a triple sharp. Triple sharps are rarely encountered except in abstract theory exercises.
  • Example 8.7.6E: Because G-double flat/B-double flat is a major third, raising the bottom note from G-double flat to G-flat makes the interval a minor third.

One easy way you can interpret this shortcut is that if the accidentals on C/E, F/A, or G/B do not match, the interval will be a minor third if the top accidental is a half-step lower than the bottom accidental.

All-White-Key Major Thirds

Thirds with C, F, and G on the bottom are the three all-white-key major thirds: C/E, F/A, and G/B.

  • When they share the same accidentals, they are major thirds.
  • When the top note has an accidental that is half-step lower than the bottom note, they are minor thirds.
  • When the bottom note has an accidental that is a half-step higher than the top note, they are minor thirds.

Practice 8.7A

Directions:

  • Identify the interval as quickly as possible using the all-white-key method.

Number 1, C-double sharp to E-double sharp. Number 2, C-double sharp to E-sharp. Number 3, C-flat to E-flat. Number 4, C-flat to E-double flat. Number 5, C-sharp to E. Number 6, F-sharp to A-sharp. Number 7, F-sharp to A. Number 8, F-double sharp to A-sharp. Number 9, F-double flat to A-double flat. Number 10, F-flat to A-double flat. Number 11, F-flat to A-flat. Number 12, G to B-flat. Number 13, G-flat to B-flat. Number 14, G-sharp to B. Number 15, G-sharp to B-sharp. Number 16, G-flat to B-double flat. Number 17, G-double sharp to B sharp.

Click here to watch the tutorial.

Solution
1) M3
2) m3
3) M3
4) m3
5) m3
6) M3
7) m3
8) m3
9) M3
10) m3
11) M3
12) m3
13) M3
14) m3
15) M3
16) m3
17) m3

Practice 8.7B

Directions:

  • Quickly write melodic intervals above the given note using half notes. Remember that you cannot change the given note.

Number 1, minor third above C-flat. Number 2, major third above C-double flat. Number 3, minor third above C-sharp. Number 4, major third above C-sharp. Number 5, major third above F-sharp. Number 6, minor third above F-sharp. Number 7, minor third above F-double sharp. Number 8, major third above F-flat. Number 9, minor third above F-flat. Number 10, minor third above G. Number 11, major third above G-flat. Number 12, minor third above G-sharp. Number 13, minor third above G-double sharp. Number 14, major third above G-double flat.

Click here to watch the tutorial.

Minor Thirds

The other thirds formed on the white keys of the piano are minor thirds.

Example 8.7.7. Thirds

C to E is a major third. D to F is a minor third. E to G is a minor third. F to A is a major third. G to B is a major third. A to C is a minor third. B to D is a minor third. The four minor thirds (from bottom notes D, E, A, and B) are boxed.

There are four all-white-key minor thirds: D/F, E/G, A/C, and B/D. This means that if accidentals match on these pairs of notes, they are minor thirds. There are several ways to remember the all-white-key minor thirds:

  • The four bottom notes spell “BEAD.”
  • The three all-white-key major thirds have C, F, and G on the bottom. Therefore, all other notes on the bottom create a minor third.

Example 8.7.8. Minor thirds

Example A shows D to F is a minor third. Example B shows that D-sharp to F-sharp is a minor third. Example C shows that D-flat to F-flat is a minor third. Example D shows that D-double sharp to F-double sharp is a minor third. Example E shows that D-double flat to F-double flat is a minor third.

All the examples in Example 8.7.8 are minor thirds. Because we know D/F is a minor third, it means that any combination of the same accidentals will also be a minor third.

Just as we transformed major thirds into minor thirds, we can also convert minor thirds into major thirds. This time, we do the opposite procedure: you can either raise the top note by a half step, or lower the bottom note a half step.

We can visualize these transformations on a keyboard.

Example 8.7.9. Transforming intervals on a keyboard

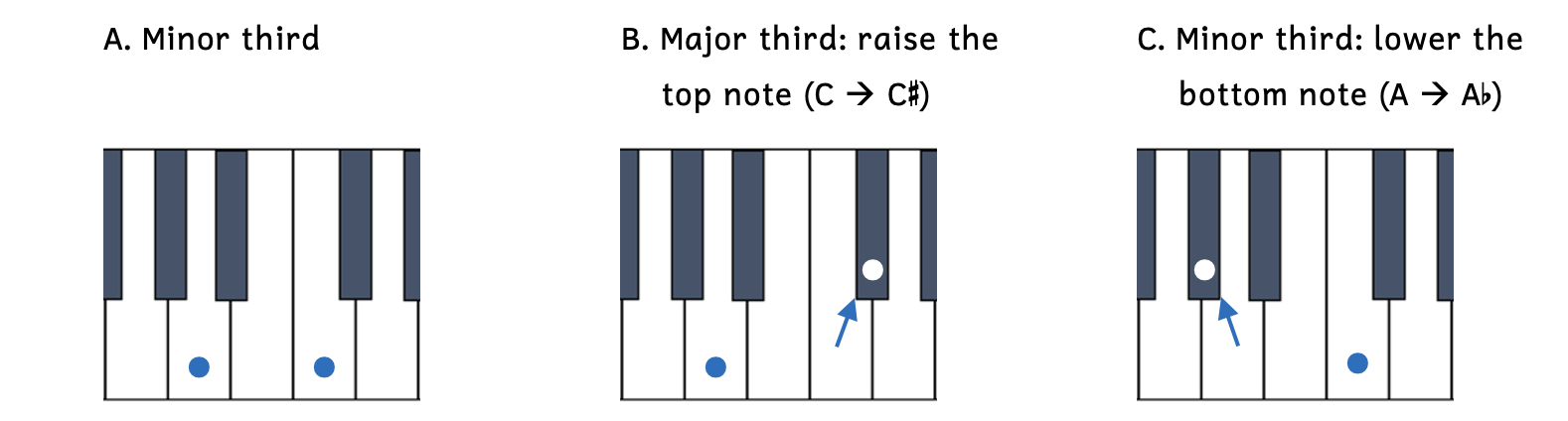
Example A shows A and C singled out on a keyboard. Example B raises C to C-sharp to create a major third. Example C lowers A to A-flat to create a major third.

  • Example 8.7.9A: A to C is an all-white-key minor third.
  • Example 8.7.9B: A to C-sharp is a major third because the top note (C) has been raised by a half step to C-sharp.
  • Example 8.7.9C: A-flat to C is also a major third, but this time it is because the bottom note (A) has been lowered by a half step to A-flat.

Once again, students usually grasp the concept of raising the top note to make an interval larger, but sometimes struggle with the idea that lowering the bottom note also makes an interval larger. They often associate flats with making an interval smaller. However, if the bottom is lowered, the space becomes larger.

Example 8.7.10. Making an interval larger

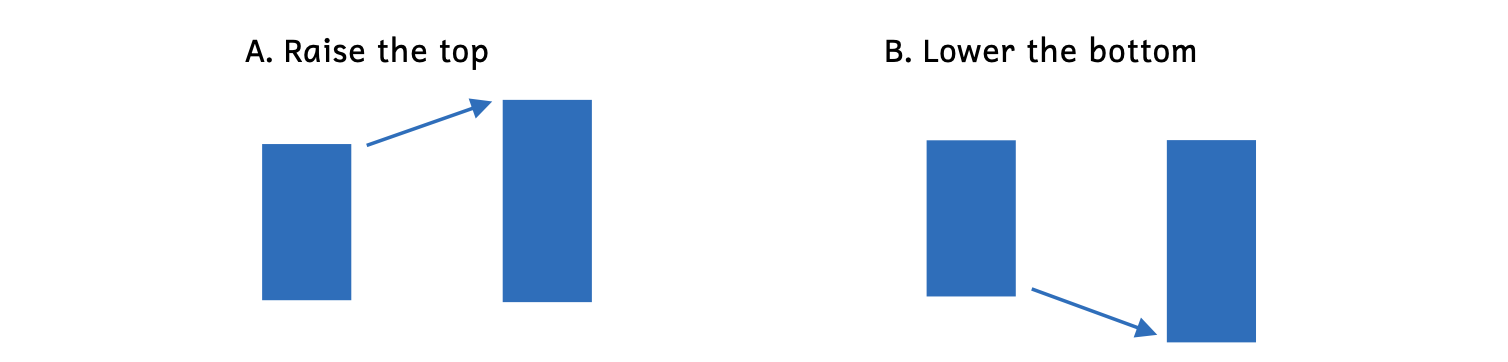
Example A shows how raising the top of a rectangle makes the rectangle larger. Example B shows how lowering the bottom of a rectangle makes the rectangle larger.

In Example 8.7.10, notice how the second rectangle in both examples is larger.

  • Example 8.7.10A: Raising the top makes the rectangle larger.
  • Example 8.7.10B: Lowering the bottom also makes the rectangle larger.

In order to quickly transform minor thirds on B, E, A and D into major thirds, we can raise the top note by a half step or lower the bottom note by a half step.

Example 8.7.11. Minor thirds to major thirds

Example A1 shows the minor third from D to F. Example A2 raises F to F-sharp, forming a major third. Example A3 lowers D to D-flat, forming a major third. Example B1 shows a minor third from D-sharp to F-sharp. Example B2 raises F-sharp to F-double sharp, forming a major third. Example B3 lowers D-sharp to D, forming a major third. Example C1 shows the minor third from D-flat to F-flat. Example C2 raises F-flat to F, forming a major third. Example C3 lowers D-flat to F-double flat, forming a major third.

  • Example 8.7.11A:
    • A1: D/F is a minor third.
    • A2: Raising the top note from F to F-sharp makes it a major third.
    • A3: Lowering the bottom note from D to D-flat makes it major third.
  • Example 8.7.11B:
    • B1: Because D/F is a minor third, D-sharp/F-sharp is also a minor third.
    • B2: Raising the top note from F-sharp to F-double sharp makes it a major third.
    • B3: Lowering the bottom note from D-sharp to D makes it major third.
  • Example 8.7.11C:
    • C1: Because D/F is a minor third, D-flat/F-flat is also a minor third.
    • C2: Raising the top note from F-flat to F makes it a major third.
    • C3: Lowering the bottom note from D-flat to D-double flat makes it major third.

We can use the all-white-key method to quickly identify thirds, such as in Example 8.7.12.

Example 8.7.12. Abrahms, “A Smile and a Tear”

Abram's "A Smile and a Tear" has a number of major thirds and minor thirds.

At first glance, the thirds in Example 8.7.12 may appear to be all-white-key intervals. However, the key signature indicates that B is flatted. Since B to D is a minor third, B-flat to D (with an asterisk) is a major third because lowering the bottom note increases the interval’s size.

One easy way you can interpret this shortcut is that if the accidentals on D/F, E/G, A/C, or B/D do not match, the interval will be a major third if the top accidental is a half-step higher than the bottom accidental.

All-White-Key Minor Thirds

Thirds beginning on D, E, A, and B (BEAD) are the four all-white-key minor thirds: D/F, E/G, A/C, and B/D.

  • When they share the same accidentals, they are minor thirds.
  • When the top note has an accidental that is half-step higher than the bottom note, they are major thirds.
  • When the bottom note has an accidental that is a half-step lower than the top note, they are major thirds.

Practice 8.7C

Directions:

  • Identify the interval as quickly as possible using the white-key method.

Number 1, D up to F-sharp. Number 2, D-flat up to F. Number 3, E-flat up to G-flat. Number 4, E-flat up to G. Number 5, E up to G-sharp. Number 6, A up to C. Number 7, A-flat up to C. Number 8, A-flat up to C-flat. Number 9,, B-sharp up to D-sharp. Number 10, B-sharp up to D-double flat. Number 11, B-double flat up to D-double flat. Number 12, D-double flat up to F-double flat. Number 13, D-flat up to F-flat. Number 14, D-double flat up to F-flat. Number 15, B up to D. Number 16, B up to D-sharp. Number 17, B-flat up to D.

Click here to watch the tutorial.

Solution
1) M3
2) M3
3) m3
4) M3
5) M3
6) m3
7) M3
8) m3
9) m3
10) M3
11) m3
12) m3
13) m3
14) M3
15) m3
16) M3
17) M3

Practice 8.7D

Directions:

  • Quickly write melodic intervals above the given note using half notes. Remember that you cannot change the given note.

Number 1, major third above B-double flat. Number 2, minor third above B-double flat. Number 3, minor third above B-flat. Number 4, minor third above D-sharp. Number 5, major third above D-sharp. Number 6, minor third above D-double sharp. Number 7, minor third above E-flat. Number 8, major third above E-flat. Number 9, major third above E-sharp. Number 10, minor third above A-sharp. Number 11, major third above A-double flat. Number 12, major third above A. Number 13, major third above A-flat. Number 14, minor third above A-double sharp.

Click here to watch the tutorial.

Half Steps

There is one last shortcut for minor thirds and major thirds. Once you have the thirds written in, you can count half steps. Although this technique will ultimately get you to the answer, it is similar to using your fingers to solve addition problems. Because it is so time consuming, the author discourages the use of this method unless the intervals are extremely tricky.

  • Minor third: three half steps
  • Major third: four half steps

Again, you must remember to write in the thirds first.

Major and Minor Thirds Using Half Steps

  • Major thirds are made of four half steps.
  • Minor thirds are made of three half steps.

Practice 8.7E

Directions:

  • Identify the interval as quickly as possible using the white-key method.

Number 1, D to F-sharp. Number 2, F# to A. Number 3, B to D. Number 4, C to E-flat. Number 5, E-flat to G. Number 6, A-flat to C-flat. Number 7, C-sharp to E-sharp. Number 8, E to G. Number 9, G-flat to B-flat. Number 10, D-flat to F. Number 11, B-flat to D-flat. Number 12, F to A. Number 13, G-sharp to B. Number 14, A to C-sharp. Number 15, D to F. Number 16, F to A-flat. Number 17, E-double sharp to G-double sharp. Number 18, C-sharp to E.

Click here to watch the tutorial.

Solution
1) M3
2) m3
3) m3
4) m3
5) M3
6) m3
7) M3
8) m3
9) M3
10) M3
11) m3
12) M3
13) m3
14) M3
15) m3
16) m3
17) m3
18) m3

Practice 8.7F

Directions:

  • Quickly write melodic intervals above the given note using half notes. Remember that you cannot change the given note.

Number 1, minor third above B. Number 2, major third above F-sharp. Number 3, major third above C-flat. Number 4, minor third above G. Number 5, minor third above D-flat. Number 6, minor third above F. Number 7, major third above D. Number 8, major third above B-flat. Number 9, minor third above E-flat. Number 10, major third above A-flat. Number 11, minor third above C-double sharp. Number 12, minor third above B-sharp. Number 13, major third above G-sharp. Number 14, minor third above A-double flat. Number 15, major third above E.

Click here to watch the tutorial.

Practice 8.7G

Directions:

  • On the score, identify and label all the harmonic thirds in the following example.

Bosmans, Impressions for Cello and Piano, I. Cortège

Score of Bosmans, Cortège for Cello and Piano.

Click here to watch the tutorial.

Practice 8.7H

Directions:

  • Using the shortcuts you learned in this chapter, identify the interval as quickly as possible.

Number 1, F-sharp to C-sharp. Number 2, G-sharp to A. Number 3, B-flat to D. Number 4, A to D. Number 5, D-flat to F-flat. Number 6, C-sharp to D-sharp. Number 7, E-flat to F. Number 8, A-flat to E-flat. Number 9. C-sharp to C-sharp. Number 10, F-sharp to A. Number 11, D-sharp to E. Number 12, G-double flat to B-double flat. Number 13, A-sharp to A-sharp. Number 14, C to E-flat. Number 15, B to C. Number 16, F to B-flat. Number 17,, D to F-sharp. Number 18, D-double sharp to A-double sharp.

Click here to watch the tutorial.

Solution
1) P5
2) m2
3) M3
4) P4
5) m3
6) M2
7) M2
8) P5
9) P1
10) m3
11) m2
12) M3
13) P8
14) m3
15) m2
16) P4
17) M3
18) P5

Practice 8.7I

Directions:

  • Quickly write the intervals above the given note. Remember that you cannot change the given note.
    • For #1-#6, write harmonic intervals using whole notes.
    • For #7-#16, write melodic intervals using half notes.

Number 1, minor second above G. Number 2, major third above C. Number 3,, perfect fifth above B-flat. Number 4, minor third above F-sharp. Number 5, perfect octave above A-flat. Number 6, major second above E. Number 7, major third above B. Number 8, perfect fourth above C-sharp. Number 9, major third above G-flat. Number 10, minor second above minor second. Number 11, perfect fifth above A-double flat. Number 12, minor third above D-flat. Number 13, perfect fourth above F. Number 14, major second above A. Number 15, major third above A-sharp. Number 16, perfect fifth above D-sharp.

Click here to watch the tutorial.

8.8  ANALYSIS: DELIBES, LAKMÉ

Léo Delibes’s famous Flower Duet begins with a beautiful melody with only stepwise motion.

Example 8.8.1. Melody from Delibes[16], “Sous le dôme épai,” Lakmé (“Flower Duet”), Act 1, Scene 2

Melody from Delibes's Flower Duet

Composers will often harmonize a melody with thirds. Recall that a harmonic interval is when two notes are sounded simultaneously. Harmonizing a melody means to have a different note or different notes sounding at the same time as the melody. Observe how Delibes harmonizes the melody from Example 8.8.1.

Example 8.8.2. Harmonized melody: Delibes, “Sous le dôme épai,” Lakmé (“Flower Duet”), Act 1, Scene 2[17]

Score to Delibes "Flower Duet"

The two sopranos do not always change notes at the same time. However, notice that whenever they do, not only are the lyrics the same, but they are always singing in thirds. In particular, every interval between the two voices in the last two measures are thirds. Listen to the example and how beautiful the thirds sound together. It seems like harmonizing a melody with only thirds would sound boring. But when we look more closely, we see why it is anything but boring.

Example 8.8.3. Intervals in Delibes, “Sous le dôme épai,” Lakmé (“Flower Duet”), Act 1, Scene 2

Thirds alternate between major thirds and minor thirds in Delibes' Flower Duet

Example 8.8.3 shows the precise intervals in measures 3-4. Notice that althought they are all thirds, there is a good mix of both major thirds and minor thirds. The variety of interval qualities creates diversity within the same interval number.

SUMMARY

  1. There are two parts to every interval label: the quality and the interval number. Always identify the interval number first. [8.1]
  2. It is helpful to memorize the intervals in the major scale when paired with the tonic: [8.2]
    • Perfect unison (P1)
    • Major second (M2)
    • Major third (M3)
    • Perfect fourth (P4)
    • Perfect fifth (P5)
    • Major sixth (M6)
    • Major seventh (M7)
    • Perfect octave (P8)
  3. The shortcut for perfect fourths and perfect fifths is that the accidentals will match unless the notes are F/B (for fourths) or B/F (for fifths). [8.3]
    • Either B will have a flat (F and B-flat or B-flat and F) or F will have a sharp (F-sharp and B or B and F-sharp).
  4. For minor intervals, you can either begin with major intervals and lower the top note, or you can start from the natural minor scale. The intervals in the natural minor scale when paired with the tonic are as follows: [8.4]
    • Perfect unison (P1)
    • Major second (M2)
    • Minor third (m3)
    • Perfect fourth (P4)
    • Perfect fifth (P5)
    • Minor sixth (m6)
    • Minor seventh (m7)
    • Perfect octave (P8)
  5. The shortcut for minor seconds and major seconds is that they are diatonic steps. [8.5]
    • Minor seconds are diatonic half steps.
    • Major seconds are diatonic whole steps.
  6. Sometimes intervals will have a tricky bottom note. When this happens, adjust the bottom note to a natural note and adjust the top note at the same proportion. [8.6]
  7. The shortcut for thirds is that thirds with C, F, or G on the bottom are all-white-key major thirds and that thirds with D, E, A, or B (BEAD) on the bottom are all-white-key minor thirds. [8.7]
  8. Being able to identify and write intervals quickly will help you a great deal in music theory.
  9. Harmonizing a melody is when another note or notes are sounded at the same time as the melody. Thirds are a common interval with which to harmonize a melody. [8.8]
  10. In Delibes’s famous “Flower Duet,” he harmonizes a beautiful melody in thirds. [8.8]

TERMS

 

 

  1. When we learn about writing for four voices, the order of notes will change. ↵
  2. Mathilde von Rothschild (1882-1924) was a German composer. ↵
  3. Alban Berg (1885-1935) was an Austrian composer. ↵
  4. Clara Wieck Schumann (1819-1896) was a German composer and pianist. Her husband was also a composer. ↵
  5. Amy Beach (1867-1944) was an American composer and pianist. ↵
  6. The tenor sounds an octave lower that what is shown. ↵
  7. Harriet Abrahms (1758-1822) was an English composer and soprano. ↵
  8. Louise Reichardt (1779-1826) was a German composer and choral conductor. ↵
  9. Henriëtte Bosmans (1895-1952) was a Dutch composer and pianist. ↵
  10. Alexander Scriabin (1872-1915) was a Russian composer and pianist. ↵
  11. Richard Strauss (1864-1949) was a German composer. ↵
  12. Louise Farrenc (1804-1875) was a French composer and pianist. ↵
  13. Lili Boulanger (1893-1918) was a French composer. ↵
  14. Sofia Zybina (?-1897) was a Russian composer. ↵
  15. Teresa Carreño (1853-1917) was a Venezuelan composer, pianist, singer, and conductor. ↵
  16. Léo Delibes (1836-1891) was a French composer. ↵
  17. Translation from www.opera-arias.com/delibes/lakme/viens-mallika. ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Steps to Music Theory Copyright © 2022 by Susan de Ghizé is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book