9 Intervals II: Further Concepts
We already learned about the most basic types of intervals. In this chapter, we will learn about all the other intervals, compound intervals, inversions, and consonance and dissonance.
9.1 OTHER QUALITIES
We learned that when you increase a minor interval by a half step while maintaining its interval number, it becomes a major interval; we also learned that when you decrease a major interval by a half step while maintaining its interval number, it becomes a minor interval. However, what happens when you increase a major interval by a half step? Or when you decrease a minor interval by a half step? What happens when a perfect interval becomes smaller or larger?
Recall that when we learned about the harmonic minor scale (Chapter 6, Section 9), there was a large gap between ![]() (le) and
(le) and ![]() (ti). In Example 9.1.1, the large gap is between B
(ti). In Example 9.1.1, the large gap is between B![]() and C
and C![]() .
.
Example 9.1.1. Harmonic minor scale

The space between ![]() (le) and
(le) and ![]() (ti) is neither a half step nor a whole step: the interval is larger than a whole step. Indeed, the harmonic minor scale contains what is called an augmented second.
(ti) is neither a half step nor a whole step: the interval is larger than a whole step. Indeed, the harmonic minor scale contains what is called an augmented second.
Interval qualities outside the realm of perfect, major, and minor are called augmented and diminished intervals. Notice the two paths interval qualities can take (Example 9.1.2).
Example 9.1.2. Other qualities

- Recall that certain interval numbers can only be perfect, while others can only be major or minor. The chart above shows how the path taken by a perfect interval differs from the path taken by a minor/major interval.
- Diminished interval (o): when a perfect interval or minor interval is reduced by a half step.
- Augmented interval (+): when a perfect interval or major interval is increased by a half step.
- The perfect intervals include the perfect unison (P1), perfect fourth (P4), perfect fifth (P5), and perfect octave (P8).
- When a perfect interval decreases by a half step, it never becomes minor. It becomes diminished.
- A half-step smaller than a perfect fifth (P5) is a diminished fifth (o5).
- A half-step larger than a perfect fourth (P4) is an augmented fourth (+4).
- The minor and major intervals include the minor/major second (m2/M2), minor/major third (m3/M3), minor/major sixth (m6/M6), and minor/major seventh (m7/M7).
- A half-step smaller than a minor seventh (m7) is a diminished seventh (o7).
- A half-step larger than a major sixth (M6) is an augmented sixth (+6).
- Notice that an augmented interval is only one half-step larger than a perfect interval while it is two half-steps larger than a minor interval.
You may also abbreviate diminished as “d” or “dim.” and augmented as “A” or “aug.” For this book, we will be using o for diminished and + for augmented.
Recall that there are two ways to make an interval smaller by a half step: lower the top note or raise the bottom note. In order to make a perfect or minor interval into a diminished interval, you can use either method.
Example 9.1.3. Diminished intervals

- Example 9.1.3A1: C to G is a perfect fifth.
- Example 9.1.3A2: When the top note G is lowered to G
 , it creates a diminished fifth (o5).
, it creates a diminished fifth (o5). - Example 9.1.3A3: When the bottom note C is raised to C
 , it creates a diminished fifth (o5).
, it creates a diminished fifth (o5).
- Example 9.1.3A2: When the top note G is lowered to G
- Example 9.1.3B1: B
 to G
to G is a minor sixth. Notice that for diminished intervals, we began with the minor sixth and not the major sixth. If we began with the major sixth, we would need to make the interval smaller by a whole step (i.e., two half steps).
is a minor sixth. Notice that for diminished intervals, we began with the minor sixth and not the major sixth. If we began with the major sixth, we would need to make the interval smaller by a whole step (i.e., two half steps).
- Example 9.1.3B2: When the top note G
 is lowered to G
is lowered to G , it creates a diminished sixth (o6).
, it creates a diminished sixth (o6). - Example 9.1.3B3: When the bottom note B
 is raised to B, it creates a diminished sixth (o6).
is raised to B, it creates a diminished sixth (o6).
- Example 9.1.3B2: When the top note G
There are two ways to make an interval bigger by a half step: raise the top note or lower the bottom note. In order to make a perfect or major interval into an augmented interval, you can use either method.
Example 9.1.4. Augmented intervals
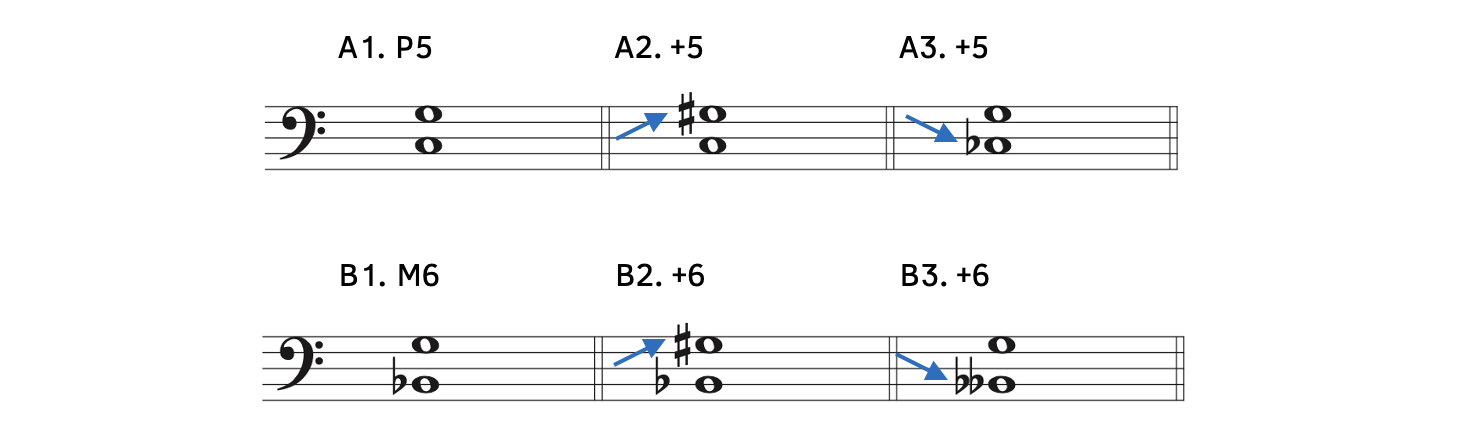
- Example 9.1.4A1: C to G is a perfect fifth.
- Example 9.1.4A2: When the top note G is raised to G
 , it creates an augmented fifth (+5).
, it creates an augmented fifth (+5). - Example 9.1.4A3: When the bottom note C is lowered to C
 , it creates an augmented fifth (+5).
, it creates an augmented fifth (+5).
- Example 9.1.4A2: When the top note G is raised to G
- Example 9.1.4B1: B
 to G is a major sixth. Notice that for augmented intervals, we begin with the major sixth and not the minor sixth. If we begin with the minor sixth, we would need to make the interval larger by a whole step (i.e., two half steps).
to G is a major sixth. Notice that for augmented intervals, we begin with the major sixth and not the minor sixth. If we begin with the minor sixth, we would need to make the interval larger by a whole step (i.e., two half steps).
- Example 9.1.4B2: When the top note G is raised to G
 , it creates an augmented sixth (+6). Notice that both a sharp and flat appear in this example. Although mixing flats and sharps do not occur with perfect, major, and minor intervals, you may encounter this mixture with augmented and diminished intervals.
, it creates an augmented sixth (+6). Notice that both a sharp and flat appear in this example. Although mixing flats and sharps do not occur with perfect, major, and minor intervals, you may encounter this mixture with augmented and diminished intervals. - Example 9.1.4B3: When the bottom note B
 is lowered to B
is lowered to B , it creates an augmented sixth (+6).
, it creates an augmented sixth (+6).
- Example 9.1.4B2: When the top note G is raised to G
If you begin with a major interval and make it diminished, or if you begin with a minor interval and make it augmented, it requires a reduction or increase of two half steps instead of one.
Example 9.1.5. Changing intervals by two half steps
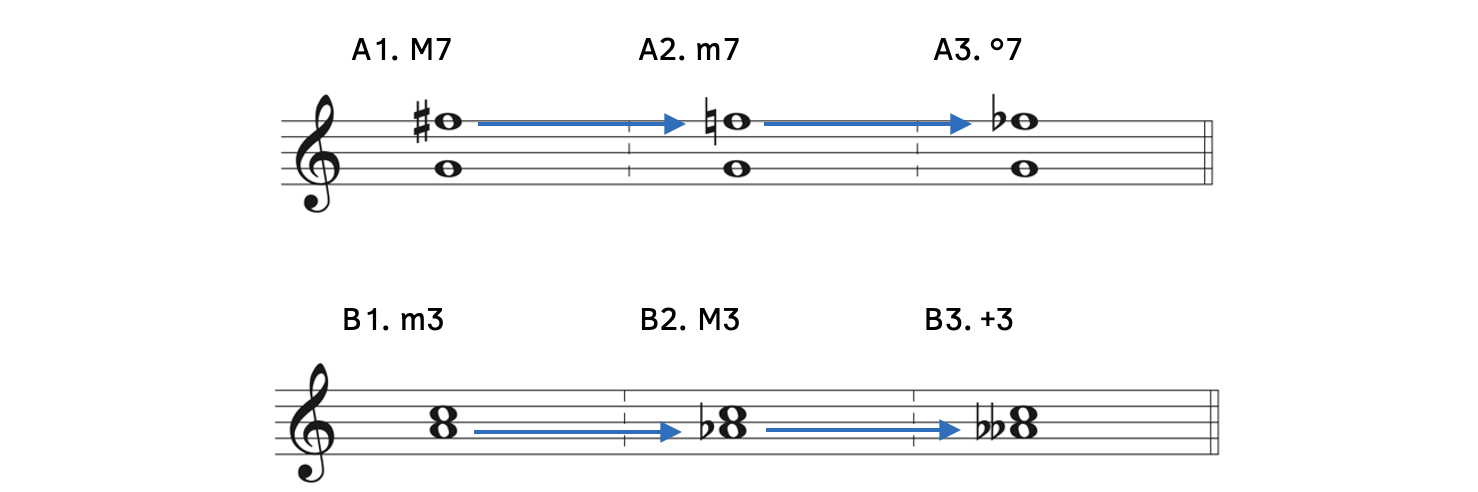
- Example 9.1.5A:
- Example 9.1.5A1: G to F
 is a major seventh. In order to create a diminished seventh, you must lower the top note by two half steps or raise the bottom note by two half steps.
is a major seventh. In order to create a diminished seventh, you must lower the top note by two half steps or raise the bottom note by two half steps. - Example 9.1.5A2: Lowering the top note from F
 to F creates a minor seventh.
to F creates a minor seventh. - Example 9.1.5A3: Lowering the top note one more time from F to F
 creates a diminished seventh.
creates a diminished seventh.
- Example 9.1.5A1: G to F
- Example 9.1.5B:
- Example 9.1.5B1: A to C is a minor third. In order to create an augmented third, you must raise the top note by two half steps or lower the bottom note by two half steps.
- Example 9.1.5B2: Lowering the bottom note from A to A
 creates a major third.
creates a major third. - Example 9.1.5B3: Lowering the bottom note one more time from A
 to A
to A creates an augmented third.
creates an augmented third.
Augmented and diminished intervals can be overwhelming for students. Always begin with what you know (i.e., perfect, major, and minor intervals) and work from there.
Augmented and Diminished Intervals
- Diminished → Perfect → Augmented
- Diminished → Minor → Major → Augmented
Identifying Other Qualities
While identifying intervals, you may come across an interval that is not perfect, major, or minor. In these cases, the interval will be augmented or diminished.
Example 9.1.6. Identifying other qualities

Step one: Find the numeric interval.
Example 9.1.7. Step one

- Example 9.1.7A: This interval is a fifth.
- Example 9.1.7B: This interval is a sixth.
Step two: Decide if the top note is more closely related to the major or minor key of the bottom note. From there, determine if the interval is larger (augmented) or smaller (diminished).
Example 9.1.8. Step two

- Example 9.1.8A: In both B major and B minor, a perfect fifth (P5) above B is F
 . Since the top note is F
. Since the top note is F , it creates an interval smaller than a perfect fifth, therefore resulting in a diminished fifth (o5).
, it creates an interval smaller than a perfect fifth, therefore resulting in a diminished fifth (o5). - Example 9.1.8B: In A
 major, a major sixth (M6) above A
major, a major sixth (M6) above A is F. Since the top note is F
is F. Since the top note is F , it creates an interval larger than a major sixth, resulting in an augmented sixth (+6).
, it creates an interval larger than a major sixth, resulting in an augmented sixth (+6).
- Alternatively, you could begin in A
 minor, where a minor sixth (m6) above A
minor, where a minor sixth (m6) above A is F
is F .
.
- Raising F
 to F
to F results in a major sixth.
results in a major sixth. - Raising F
 to F
to F results in an augmented sixth, which is the answer.
results in an augmented sixth, which is the answer.
- Raising F
- In this case, beginning with A
 major would have been quicker.
major would have been quicker.
- Alternatively, you could begin in A
You may have noticed that Example 9.1.8B contained both a flat and a sharp. One shortcut you can use is that only augmented and diminished intervals will have both types of accidentals.
Augmented and diminished intervals are often (but not always) tricky intervals. However, do not be intimidated and take it step by step. Just as we did with tricky intervals, temporarily change the bottom note to a note that has a major or minor key. Apply the same transformation to the top note, then identify the interval.
Example 9.1.9. Identifying other qualities with tricky notes
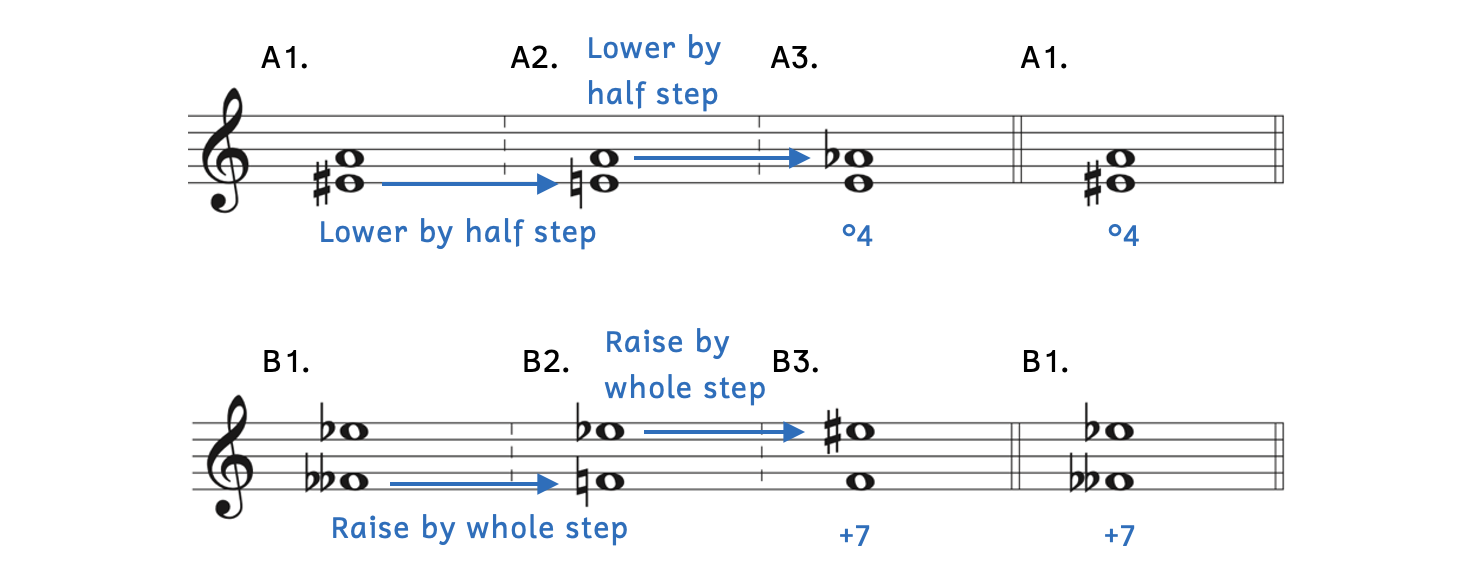
- Example 9.1.9A:
- Example 9.1.9A1: There is no such key as E
 major or E
major or E minor.
minor. - Example 9.1.9A2: Lower E
 by a half step to become E
by a half step to become E –a key we are familiar with.
–a key we are familiar with. - Example 9.1.9A3:
- Apply the same transformation to the top note: Lower the top note (A) by a half step to A
 .
. - The interval from E to A is a perfect fourth (P4). Lowering the top note (A
 ) makes the interval smaller, thus creating a diminished fourth (o4).
) makes the interval smaller, thus creating a diminished fourth (o4).
- Apply the same transformation to the top note: Lower the top note (A) by a half step to A
- Example 9.1.9A1: Returning to the original notes (E
 to A), we transfer our answer: o4.
to A), we transfer our answer: o4. - Alternatively, we could use the shortcut for perfect fourths:
- Since the interval is a fourth and notes are not F and B, we know that E to A is a perfect fourth (P4).
- Raising the bottom note makes the interval smaller, resulting in a diminished fourth (o4).
- Example 9.1.9A1: There is no such key as E
- Example 9.1.9B:
- Example 9.1.9B1: There is no such key as F
 major or F
major or F minor.
minor. - Example 9.1.9B2: Raise F
 a whole step to become F–a key we are familiar with.
a whole step to become F–a key we are familiar with. - Example 9.1.9B3:
- Apply the same transformation to the top note: Raise the top note (E
 ) by a whole step to E
) by a whole step to E .
. - The interval from F to E is a major seventh. Raising the top note (E
 ) makes the interval larger, thus creating an augmented seventh (+7).
) makes the interval larger, thus creating an augmented seventh (+7).
- Apply the same transformation to the top note: Raise the top note (E
- Example 9.1.9B1: Returning to the original notes (F
 to E
to E ), we transfer our answer: +7.
), we transfer our answer: +7. - Play Example 9.1.9B on the piano—it sounds like an octave! However, because of the way the dyad is written, the interval is not a perfect octave, but rather, an augmented seventh.
- Example 9.1.9B1: There is no such key as F
Augmented and diminished intervals are not uncommon. Example 9.1.10 contains different types of intervals.
Example 9.1.10. Other intervals: Cournand[1], Waltz in A Major

- Example 9.1.10A: There is a harmonic diminished fifth (o5).
- The quickest way to identify this interval is by using the perfect fifth shortcut. E to B is a perfect fifth (same accidentals and the notes are not B and F) and E
 raises the bottom, making the interval smaller. Therefore, the interval is a diminished fifth (o5).
raises the bottom, making the interval smaller. Therefore, the interval is a diminished fifth (o5).
- The quickest way to identify this interval is by using the perfect fifth shortcut. E to B is a perfect fifth (same accidentals and the notes are not B and F) and E
- Example 9.1.10B: There is a melodic augmented second (+2).
- The quickest way to identify this interval is by using the major second shortcut. D to E is a major second (whole step) and E
 raises the top, making the interval larger. Therefore, the interval is an augmented second (+2).
raises the top, making the interval larger. Therefore, the interval is an augmented second (+2).
- The quickest way to identify this interval is by using the major second shortcut. D to E is a major second (whole step) and E
All interval numbers can be diminished or augmented except for the unison. The unison can be augmented but can never be diminished.
Example 9.1.11. The unison

- Example 9.1.11A: G to G is perfect unison because they are the same pitch.
- Example 9.1.11B: G to G
 is an augmented unison because G
is an augmented unison because G is a half-step larger than a perfect unison.
is a half-step larger than a perfect unison. - Example 9.1.11C: G to G
 is also an augmented unison.
is also an augmented unison.
- At first glance, it may appear than Example 9.1.11C is a diminished unison because G
 is lower than G.
is lower than G. - However, intervals are always based on the lower note. In Example 9.1.11C, the lower note is now G
 and not G.
and not G. - G
 to G
to G would be a perfect unison, and G
would be a perfect unison, and G to G is a half step larger, resulting in an augmented unison.
to G is a half step larger, resulting in an augmented unison.
- At first glance, it may appear than Example 9.1.11C is a diminished unison because G
Identifying Other Interval Qualities
- Always begin with the three basic types: perfect, major, or minor.
- From there, determine if the given interval is larger (augmented) or smaller (diminished).
- Remember that perfect intervals and major/minor intervals are on different tracks.
Writing Other Qualities
When writing augmented and diminished intervals, you must first establish if the quality of the interval number is perfect or major/minor. This is because the number of half-step alterations will vary depending on your starting point. Because fifths are perfect while sixths are major/minor, we will approach each interval differently. Let’s practice a few examples step by step.
Example 9.1.12. Write an augmented fifth above the given note
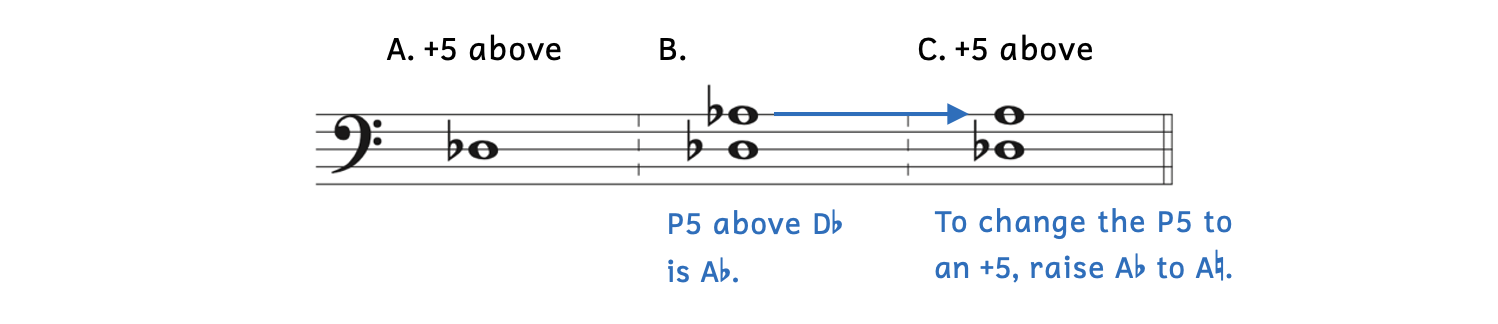
- Example 9.1.12A: Write an augmented fifth above D
 .
. - Example 9.1.12B: We know that a perfect fifth above D
 is A
is A .
. - Example 9.1.12C: In order to change the perfect fifth into an augmented fifth, raise A
 to A
to A .
.
Example 9.1.13. Write an augmented sixth above the given note
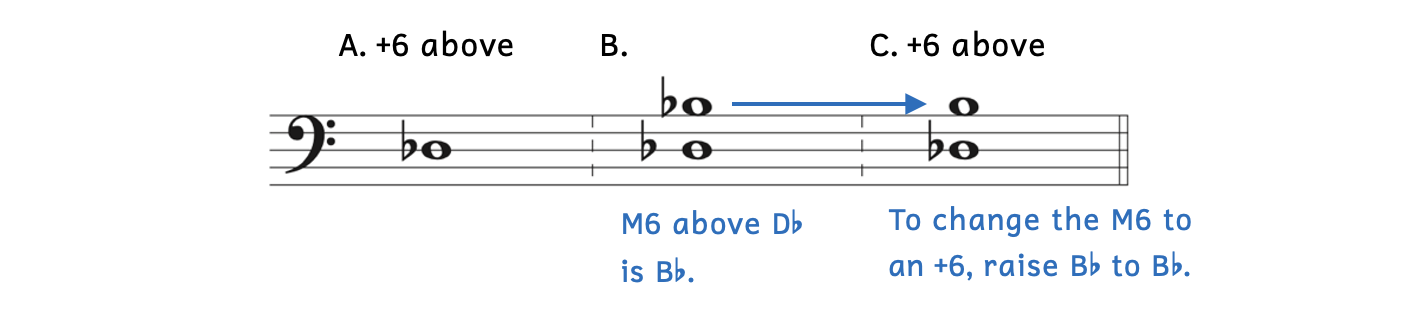
- Example 9.1.13A: Write an augmented sixth above D
 .
. - Example 9.1.13B: We begin with the key of D
 major, since there is no such key as D
major, since there is no such key as D minor. A major sixth above D
minor. A major sixth above D is B
is B .
. - Example 9.1.13C: In order to change the major sixth into an augmented sixth, raise B
 to B
to B .
.
Example 9.1.14. Write an augmented sixth above the given note.
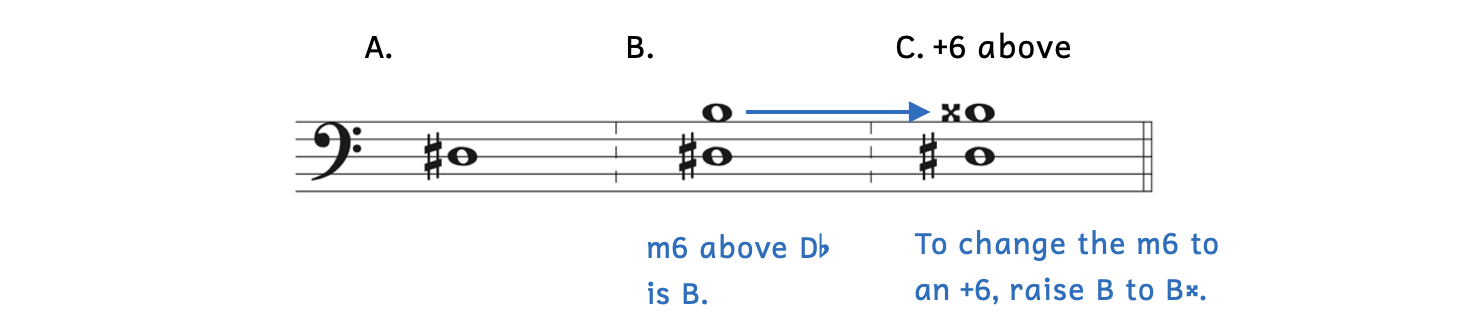
- Example 9.1.14A: The question asks to write an augmented sixth above D
 .
. - Example 9.1.14B: We begin with the key of D
 minor, as there is no such key as D
minor, as there is no such key as D major. A minor sixth above D
major. A minor sixth above D is B.
is B. - Example 9.1.14C: In order to change the minor sixth into an augmented sixth, raise B to B
 . It must be raised by two half steps when changing an interval from minor to augmented.
. It must be raised by two half steps when changing an interval from minor to augmented.
As you saw in Example 9.1.12 – 9.1.14, the number of half-step alterations vary depending on if the interval begins as minor, major, or perfect.
The best thing you can do is practice intervals as much as you can to gain fluency. The more you practice intervals, the faster you will get at combining shortcuts to come up with the correct answer. Later, we will use these intervals to build larger musical structures. Efficiently identifying intervals will be extremely helpful.
Writing Other Interval Qualities
- Write the interval number. This is always the first step when writing any interval.
- Write a closely-related basic interval: perfect, major, or minor.
- Adjust the top note with an accidental to make the interval bigger or smaller.
Practice 9.1A. Identifying Diminished and Augmented Intervals
Directions:
- Identify the intervals.

Click here to watch the tutorial.
Solution
Practice 9.1B. Writing Diminished and Augmented Intervals
Directions:
- Write the interval above the given note.
- For #1-#4 and #10-#14, write a melodic interval using half notes.
- For #5-9, write a harmonic interval using whole notes.

Practice 9.1C. Identifying Intervals in Music
Directions:
- Identify the circled intervals.
Smyth[2], Three Songs, No. 1, “The Clown”

Click here to watch the tutorial.
Solution
Practice 9.1D. Identifying Intervals (All)
Directions:
- Identify the intervals. This section includes all the intervals we have learned.

Click here to watch the tutorial.
Solution
Practice 9.1E. Writing Intervals (All)
Directions:
- Write the interval above the given note. Use the empty staff as scratch paper.
- For #1-#5, write a harmonic interval using whole notes.
- For #6-#15, write a melodic interval using half notes.

Click here to watch the tutorial.
9.2 COMPOUND INTERVALS
An interval is the distance between two notes. We have only learned about intervals up to an octave at this point, but clearly there can be intervals larger than an octave. Intervals an octave or smaller are simple intervals. Intervals larger than an octave are compound intervals.
Example 9.2.1. Simple and compound intervals
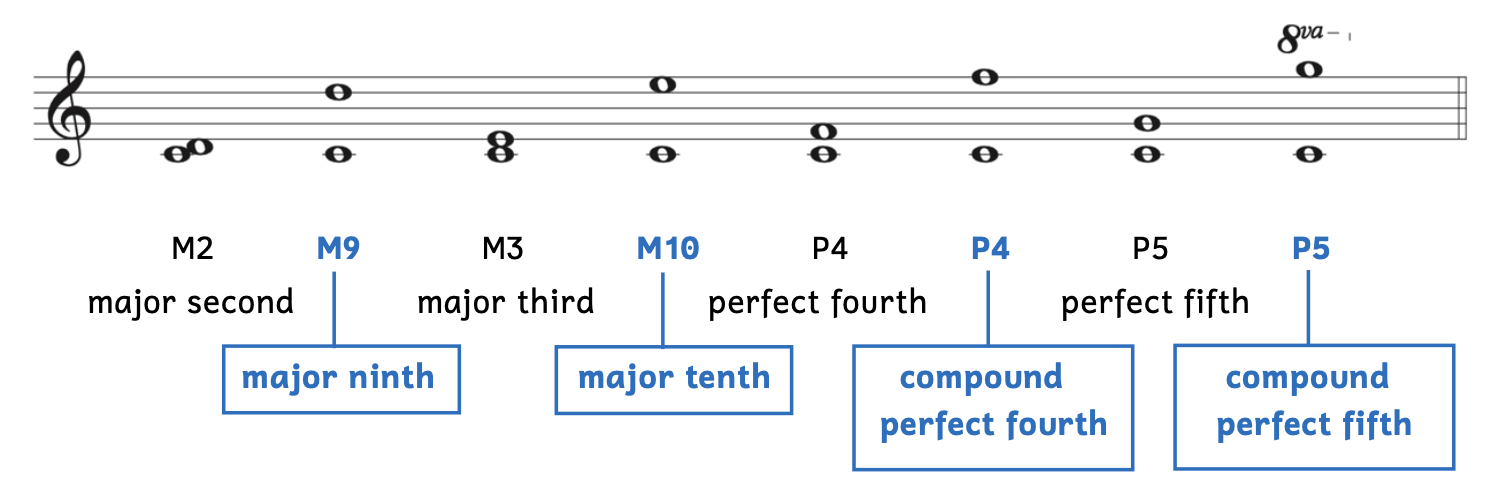
- The intervals that are in blue boxes (major ninth, major tenth, compound perfect fourth, and compound perfect fifth) are compound intervals.
- Although we can say “compound perfect fourth,” we generally only write “P4.”
- Because the ninth and tenth are fairly common, they are often referred to as a ninth and tenth. However, they can also be called a compound second and compound third.
- The compound perfect fifth (last example) is more than two octaves apart. The compound label does not distinguish between intervals one or more octaves apart.
When identifying compound intervals, compress the interval to its simple form by either lowering the top note an octave or more or raising the bottom note an octave or more until the interval is less than an octave apart. It is very important that you do not move the top note below the bottom note. Remember that intervals are always based on the bottom note, so you cannot change the bottom note.
Example 9.2.2. Identifying compound intervals
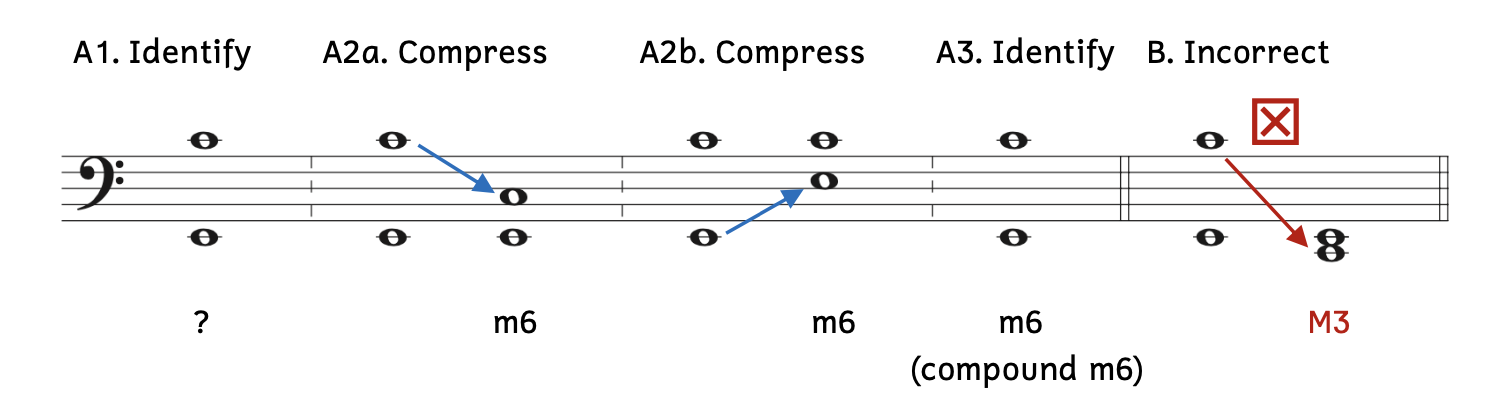
- Example 9.2.2A:
- Example 9.2.2A1: Identify the given interval.
- Example 9.2.2A2a: Lower the top note an octave from C4 to C3 to change the compound interval to a simple interval. The interval is a minor sixth (m6).
- Example 9.2.2A2b: As another option, you can raise the bottom note an octave from E2 to E3 to change the compound interval to a simple interval. The answer is the same (m6).
- Example 9.2.2A3: Although the interval is literally a compound minor sixth, you can simply write “m6.”
- Example 9.2.2B: This is a common mistake that students make. Rather than dropping only one octave, C4 is written below E2. By doing so, C2 is now the bottom note and the interval is a major third, which is incorrect. The correct answer is a minor sixth. You cannot change the bottom note.
In Example 9.2.1, the last interval was more than two octaves apart. When identifying even larger intervals, continue lowering the top note by an octave or more (or raising the lower note by an octave or more) until you create a simple interval.
Example 9.2.3. Identifying large compound intervals

- Example 9.2.3A: Identify the given interval.
- Example 9.2.3B: To compress the given compound interval to a simple interval, lower the top note (G-sharp5) until it is less than an octave above the bottom note (F2). We must lower G-sharp three octaves (G
 5 to G
5 to G 4 to G
4 to G 3 to G
3 to G 2) in order to accomplish this. Identifying the interval is now manageable: It is an augmented second (+2).
2) in order to accomplish this. Identifying the interval is now manageable: It is an augmented second (+2). - Example 9.2.3C: Although the interval is very large, we still label it as an augmented second (+2). Never label it as an augmented twenty-third (+23).
In Example 9.2.4, Scriabin fills the melody with compound intervals in his etude.
Example 9.2.4. Compound intervals in Scriabin[3], Etude, Op. 65, No. 1

At first glance, one may think that the pianist plays running octaves in their right hand. However, upon closer inspection the intervals are larger than an octave—in fact, they are major ninths (or compound major seconds).
Compound intervals are everywhere as they are not confined to one staff. Remember that when identifying compound intervals, merely compress the interval so that it is simple (an octave or smaller). Identify the compound intervals in the next example.
Example 9.2.5. Compound intervals: Strozzi[4], “Non c’è più fede”

- Every interval is a compound interval.
- Notice that the first two intervals are both perfect fifths (P5). Although the first interval is a nineteenth and the second interval is only a twelfth, they are still labeled the same.
Compound Intervals
Compound intervals are greater than an octave. To find a compound interval, compress the interval into a simple interval (i.e., an octave or smaller) while maintaining the bass (lowest note).
Practice 9.2A. Identifying Compound Intervals
Directions:
- Identify the given compound interval by its simple interval name.

Click here to watch the tutorial.
Solution
Practice 9.2B. Identifying Compound Intervals in Music
Directions:
- Identify the compound intervals between the highest and lowest notes only.
Mounsey[5], Six Four-Part Songs, Op. 30, “Serenade”

Click here to watch the tutorial.
Solution
9.3 INTERVAL INVERSIONS
Recall that when reducing compound intervals to simple intervals, it was important that we did not move the top note below the bottom note. When we move the top note below the bottom note, it created a different interval, which is the interval inversion.
Example 9.3.1. Interval Inversions
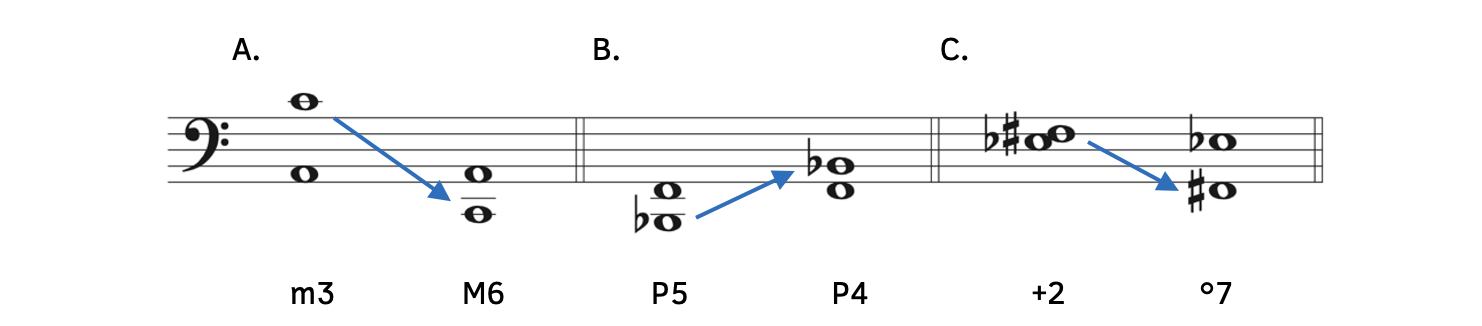
- Example 9.3.1A: When we move the top note (C4) so that it is now the bottom note (C2), the interval becomes a major sixth.
- When A is the bottom note, we think in the key of A major (or A minor). Therefore, the interval from A up to C is a minor third.
- When C is the bottom note, we think in the key of C major (or C minor). Therefore, the interval from C to A is a major sixth.
- Example 9.3.1B: The first interval is a perfect fifth. Since it is written very low, it might be difficult to read multiple ledger lines if we move the top note below the bottom note. Instead, move the bottom note above the top note. To find an interval inversion, you can move the top note below or the bottom note above—you should arrive at the same answer. When we move the bottom note (B
 1) so that it is now the top note (B
1) so that it is now the top note (B 2), the interval becomes a perfect fourth.
2), the interval becomes a perfect fourth.
- When B
 is the bottom note, we think in the key of B
is the bottom note, we think in the key of B major (or B
major (or B minor). Therefore, the interval from B
minor). Therefore, the interval from B up to F is a perfect fifth.
up to F is a perfect fifth. - When F is the bottom note, we think in the key of F major (or F minor). Therefore, the interval from F to B
 is a perfect fourth.
is a perfect fourth.
- When B
- Example 9.3.1C: The first interval is an augmented second. When we move the top note (F
 3) so that it is now the bottom note (F
3) so that it is now the bottom note (F 2), the interval becomes a diminished seventh. Be sure to rewrite the accidentals correctly.
2), the interval becomes a diminished seventh. Be sure to rewrite the accidentals correctly.
- When E
 is the bottom note, we think in the key of E
is the bottom note, we think in the key of E major (or E
major (or E minor). Therefore, the interval from E
minor). Therefore, the interval from E up to F
up to F is an augmented second.
is an augmented second. - When F
 is the bottom note, we think in the key of F
is the bottom note, we think in the key of F p major (or F
p major (or F minor). Therefore, the interval from F
minor). Therefore, the interval from F to E
to E is a diminished seventh.
is a diminished seventh.
- When E
Interval inversions are common in music, as seen in Example 9.3.2.
Example 9.3.2. Interval inversions: Beethoven[6], Symphony No. 3 in E-flat major, Op. 55, (“Eroica”), iv – Allegro molto

After a boisterous introduction, the first theme of the last movement of Beethoven’s Eroica Symphony begins with the strings, as shown in Example 9.3.2. All instruments play in unison (except for the cellos, who play an octave lower).
- Example 9.3.2A: When looking at the first pair of notes, each instrument begins with an E
 ascending to B
ascending to B , creating an interval of a perfect fifth (P5).
, creating an interval of a perfect fifth (P5). - The B
 in measure 13 then leaps down an octave in measure 14.
in measure 13 then leaps down an octave in measure 14. - Example 9.3.2B: By moving the B
 that was previously above E
that was previously above E to now be below E
to now be below E , the interval is inverted. The newly formed interval is a perfect fourth (P4).
, the interval is inverted. The newly formed interval is a perfect fourth (P4).
Interval Inversions
When we invert an interval, it means that what was the bottom note now becomes the top note (or vice versa).
Practice 9.3A. Inverting Intervals
Directions:
- Invert the given intervals on the staff.
- Write the intervals in the blanks.

Click here to watch the tutorial.
Writing Other Qualities
You may have noticed a pattern between the interval qualities and the interval numbers when writing interval inversions. Indeed, there is a shortcut that can help you identify interval inversions quickly. The inversion of interval qualities will always be as shown in Example 9.3.3.
Example 9.3.3. Inversions of interval qualities
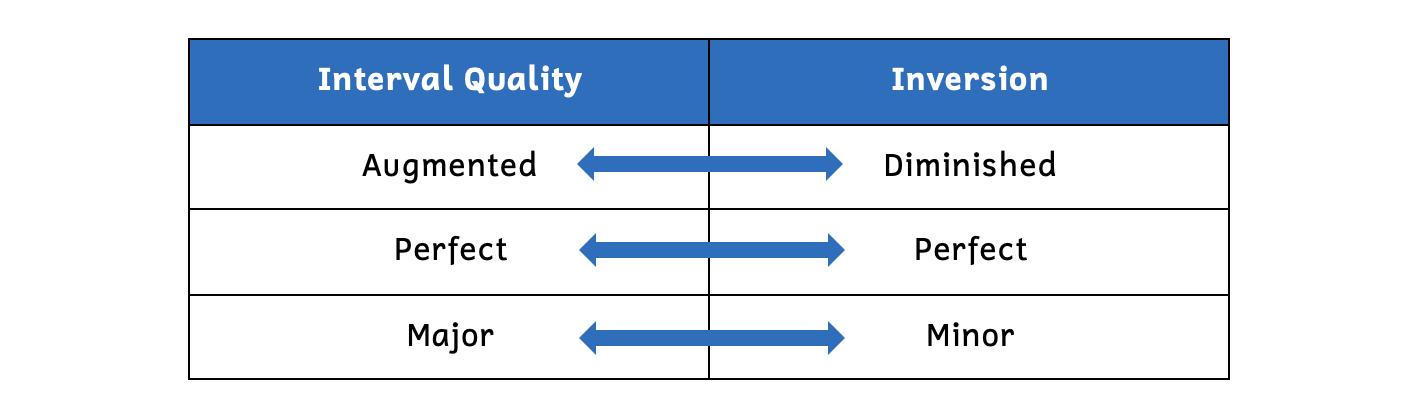
- The inversion of any augmented interval is diminished (and vice versa).
- The inversion of any perfect interval is perfect.
- The inversion of any major interval is minor (and vice versa).
The inversion of interval numbers will always add up to nine (Example 9.3.4).
Example 9.3.4. Inversions of interval numbers
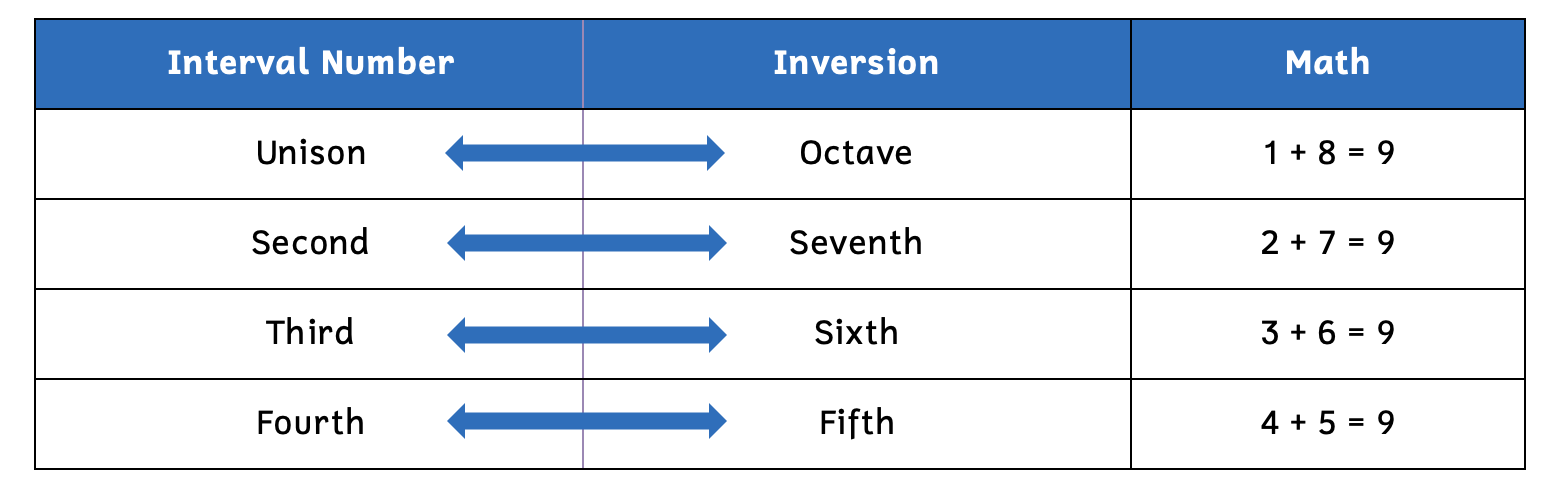
- The inversion of a unison (1) is an octave (8) (and vice versa) because 1 + 8 = 9.
- The inversion of a second (2) is a seventh (7) (and vice versa) because 2 + 7 = 9.
- The inversion of a third (3) is a sixth (6) (and vice versa) because 3 + 6 = 9.
- The inversion of a fourth (4) is a fifth (5) (and vice versa) because 4 + 5 = 9.
Knowing these shortcuts, we can quickly identify the inversion of any interval without having to figure out the interval step-by-step (Example 9.3.5).
Example 9.3.5. Samples of interval inversions
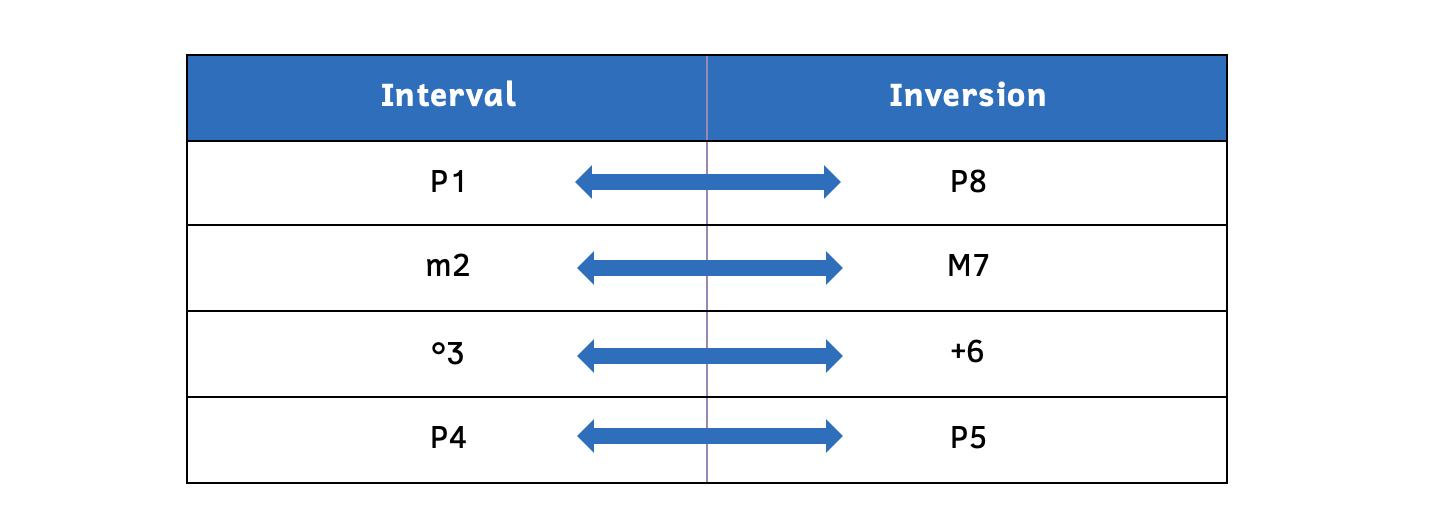
- The inversion of a perfect interval is a perfect interval, and the inversion of a unison is an octave. Therefore, the inversion of a perfect unison (P1) is a perfect octave (P8).
- The inversion of a minor interval is a major interval, and the inversion of a second is a seventh. Therefore, the inversion of a minor second (m2) is a major seventh (M7).
- The inversion of a diminished interval is an augmented interval, and the inversion of a third is a sixth. Therefore, the inversion of a diminished third (o3) is an augmented sixth (+6).
- The inversion of a perfect interval is a perfect interval, and the inversion of a fourth is a fifth. Therefore, the inversion of a perfect fourth (P4) is a perfect fifth (P5).
Shortcut: Inversions
The inversion of interval qualities:
- Augmented ↔ Diminished
- Perfect ↔ Perfect
- Major ↔ Minor
The inversion of interval numbers add up to nine:
- 1 ↔ 8
- 2 ↔ 7
- 3 ↔ 6
- 4 ↔ 5
Practice 9.3B. Shortcut: Finding Interval Inversions
Directions:
- Write the inversions of the given intervals using the shortcut.
Click here to watch the tutorial.
Solution
9.4 WRITING INTERVALS BELOW
As we learned, intervals are always based on the key signature of the bottom note. Identifying descending intervals is not complicated, as you would simply look for the lower note. However, writing intervals below a given note is sometimes a struggle for students. Example 9.4.1. shows a common error made by students.
Example 9.4.1. Common error

- Example 9.4.1A: The directions ask to write a major third below C5.
- Example 9.4.1B: A third below C is A, but it is a minor third—not a major third.
- The mistake is that students think in the key of C major, which has no flats or sharps. Indeed, A belongs to the key of C, but C is no longer the bottom note.
- The bottom note is A, and the key of A major has three sharps including C
 . Therefore, A to C is actually a minor third.
. Therefore, A to C is actually a minor third. - Remember: Intervals are always based on the lower note.
From Example 9.4.1B, students will often try to fix the error by creating another error (Example 9.4.2).
Example 9.4.2. Another common error

- Example 9.4.2A: This was the first mistake created in Ex. 9.4.1: The interval is a minor third instead of a major third.
- Example 9.4.2B: In order to fix this problem, students try to increase a minor third into a major third by raising the top note (C
 ).
).
- The problem is that the given note has been changed. The directions asked for a major third below C, not C
 .
. - Remember: You can never change the given note.
- The problem is that the given note has been changed. The directions asked for a major third below C, not C
We learned that there are two ways to increase an interval by a half step: raise the top note or lower the bottom note. Since we can never change the given note—in this case the top note—our only option is to lower the bottom note.
Example 9.4.3. Correct answer

- Example 9.4.3A: This was the first mistake created in Ex. 9.4.1: The interval is a minor third instead of a major third.
- Example 9.4.3B: In order to fix this problem, you must lower the bottom note from A to A-flat since you cannot change the given note (C).
- In the key of A-flat major, there are four flats, so C is a major third.
There are two ways to write intervals below a given note: Method #1 (Write and Adjust) and Method #2 (Using Interval Inversions).
Method #1: Write and Adjust
Writing intervals below begins with the same steps as writing intervals above, but you need an additional step.
- When being asked to write an interval below, first write in the pitch below based on the interval number.
- Identify the new interval you created, and adjust the bottom note accordingly.
We will go through two examples step by step.
Example 9.4.4. Method #1: Write and adjust

- Example 9.4.4A: The directions ask to write a minor sixth below the given note.
- Example 9.4.4B: Ignoring accidentals for now, write a generic sixth below B. In this case, the bottom note is B. Next, identify the new interval. The interval is a major sixth.
- Example 9.4.4C: Adjust the bottom interval to create the interval that is asked. In order to change a major sixth into a minor sixth, the interval must be made smaller by a half step. Since we cannot change the top note, raise the bottom note from B to B
 .
.
Example 9.4.5. Method #1: Write and adjust

- Example 9.4.5A: The directions ask to write an augmented fourth below the given note.
- Example 9.4.5B: Write a generic fourth below D. In this case, the bottom note is A. Next, identify the new interval. The interval is a perfect fourth.
- Example 9.4.5C: Adjust the bottom interval to create the interval that is asked. In order to change a perfect fourth into an augmented fourth, the interval must be made larger by a half step. Since we cannot change the top note, lower the bottom note from A to A
 .
.
Whenever you use Method #1, you must remember that you cannot change the given note—in this case, the top note.
Practice 9.4A. Writing Intervals Below by Adjusting
Directions:
- Write the harmonic intervals below the given notes using whole notes. Use Method #1: Write and Adjust.

Click here to watch the tutorial.
Method #2: Using Interval Inversions
For some students, writing intervals below is challenging because they want to change the top note. An easier way for many students is to use interval inversions.
- When being asked to write an interval below, write the interval inversion above instead.
- Once you figure out your answer, write the answer an octave lower so that your answer is below the given note.
We will go through two examples step by step.
Example 9.4.6. Method #2: Using interval inversions

- Example 9.4.6A: The directions ask to write a major third below C.
- Example 9.4.6B: The inversion of a major third is a minor sixth. Write a minor sixth above C: A
 .
. - Example 9.4.6C: Once you identify the answer, write the note (A
 ) an octave lower, so that it is below the given note.
) an octave lower, so that it is below the given note.
Example 9.4.7. Method #2: Using interval inversions

- Example 9.4.7A: The directions ask to write a diminished seventh below E
 .
. - Example 9.4.7B: The inversion of a diminished seventh is an augmented second. Write an augmented second above E
 : F
: F .
. - Example 9.4.7C: Once you identify the answer, write the note (F
 ) an octave lower, so that it is below the given note.
) an octave lower, so that it is below the given note.
By using the interval inversion, you can use a technique you have already learned: writing intervals above.
Writing Intervals Below
When asked to write an interval below a given note, there are two methods:
- Method #1: Write and Adjust
- Write the pitch below the given note based solely on the interval number.
- Identify the interval.
- Adjust the bottom note with an accidental to create the correct interval.
- Method #2: Using Interval Inversions
- Write the interval inversion above the given note.
- Transfer your answer an octave lower so that it is below the given note.
Practice 9.4B. Writing Intervals Below by Inverting
Directions:
- Write the harmonic intervals below the given notes using whole notes. Use Method #2: Using Interval Inversions and use the staff below as scratch paper.

Click here to watch the tutorial.
Practice 9.4C. Writing Intervals Below
Directions:
- Using either method, write the harmonic intervals below the given notes using whole notes. Use the staff below as scratch paper.

Click here to watch the tutorial.
9.5 SHORTCUT: m7/M7
Since sevenths are such large intervals, they sometimes create problems for students. However, you can use interval inversions for an easy way to identify and write sevenths. Recall that the inversion of a seventh is a second, and that the inversion of major is minor. When writing or identifying sevenths, we can temporarily use the inversion to help us.
- The inversion of a major seventh is a minor second.
- The inversion of a minor seventh is a major second.
We already learned a shortcut for seconds.
- A minor second is a diatonic half step.
- A major second is a diatonic whole step.
When writing sevenths, we can use interval inversions. Temporarily invert the seventh and think of a diatonic half step for a major seventh or a diatonic whole step for a minor seventh.
Example 9.5.1. Writing sevenths above using interval inversions

- Example 9.5.1A:
- Example 9.5.1A1: The directions ask for a minor seventh above B.
- Example 9.5.1A2: Because the inversion of a minor seventh is a major second, temporarily think of a major second (i.e., diatonic whole step) below B. The answer is A.
- Example 9.5.1A3: Move the A below the given B so that it is above the given B. By doing so, you have now written a minor seventh above B.
- Example 9.5.1B:
- Example 9.5.1B1: The directions ask for a major seventh above B
 .
. - Example 9.5.1B2: Because the inversion of a major seventh is a minor second, temporarily think of a minor second (i.e., diatonic half step) below B
 . The answer is A
. The answer is A .
. - Example 9.5.1B3. Move the A
 below the given B
below the given B so that it is above the given B
so that it is above the given B . By doing so, you have now written a major seventh above B
. By doing so, you have now written a major seventh above B .
.
- Example 9.5.1B1: The directions ask for a major seventh above B
Whereas writing a minor seventh above B is fairly simple since the keys of B major and B minor both exist, writing a seventh above B![]() may be more challenging and using the inversion may be useful.
may be more challenging and using the inversion may be useful.
Similarly, use the inversion of sevenths to write intervals below.
Example 9.5.2. Writing sevenths below using interval inversions

- Example 9.5.2A: The directions ask to write a major seventh below E
 .
. - Example 9.5.2B: The inversion of a major seventh is a minor second. Write a diatonic half step above E
 , which is F
, which is F .
. - Example 9.5.2C: Rewrite the F
 an octave lower so that it is now below the given note.
an octave lower so that it is now below the given note.
When identifying sevenths, you will also temporarily invert the seventh to see what kind of second is formed.
Example 9.5.3. Identifying sevenths

- Example 9.5.3A:
- Example 9.5.3A1: Because the key of F
 major or minor does not exist, we can use the inversion to identify the quality of this seventh.
major or minor does not exist, we can use the inversion to identify the quality of this seventh. - Example 9.5.3A2: When we write F
 above E
above E , we see the interval is a half step (i.e., minor second).
, we see the interval is a half step (i.e., minor second).
- Shortcut! When the accidentals are the same, we can remove both of them. The interval from E to F is a minor second.
- Example 9.5.3A3: To find the answer of the original question, you must find the inversion of a minor second, which is a major seventh.
- Example 9.5.3A1: Because the key of F
- Example 9.5.3B:
- Example 9.5.3B1: Because the key of F
 major or minor does not exist, we can use the inversion to identify the quality of this seventh.
major or minor does not exist, we can use the inversion to identify the quality of this seventh. - Example 9.5.3B2: When we write E below F
 , we see the interval is an augmented second.
, we see the interval is an augmented second.
- E to F-sharp is a major second, and F
 makes the interval a half step larger.
makes the interval a half step larger.
- E to F-sharp is a major second, and F
- Example 9.5.3B3: To find the answer of the original question, you must find the inversion of an augmented second, which is a diminished seventh.
- Example 9.5.3B1: Because the key of F
Sevenths abound in Example 9.5.4. See if you can quickly recognize the qualities of the sevenths by using the inversion of a second. Also identify the melodic sevenths in the bass clef.
Example 9.5.4. Sevenths in Scriabin, Etude, Op. 65, No. 2 – Allegretto

- All the sevenths in the treble clef are harmonic major sevenths. Some have extreme spellings (e.g., A
 and G
and G ).
). - All the sevenths in the bass clef are melodic minor sevenths. Some of these also have extreme spelling (e.g., E
 and F
and F ).
).
In the last two chapters, we have seen how Scriabin’s Etudes Op. 65 contain three fascinating examples of intervals.
- Etude Op. 65, No. 1: Ninths (Chapter 9, Section 2. Compound Intervals)
- Etude Op. 65, No. 2: Sevenths (Chapter 9, Section 5. Shortcut: m7/M7)
- Etude Op. 65, No. 3: Perfect fifths (Chapter 8, Section 3. Shortcut: P4/P5)
Etude No. 2 (Example 9.5.4) is particularly intriguing because Scriabin combines harmonic major sevenths in the right hand with melodic minor sevenths in the left hand.
Shortcut: m7/M7
Using inversions can be an easier way to identify and write sevenths. Since the inversion of a minor seventh is a major second and the inversion of a major seventh is a minor second, we can temporarily think of diatonic half steps and diatonic whole steps to find our answer.
Practice 9.5A. Shortcut: Identifying Major and Minor Sevenths
Directions:
- Identify the sevenths as quickly as you can by using the inversion method.

Click here to watch the tutorial.
Solution
Practice 9.5B. Shortcut: Writing Major and Minor Sevenths
Directions
- Quickly write the melodic seventh above or below the given note using half notes.

Click here to watch the tutorial.
Practice 9.5C. Identifying Large Intervals in Music
Directions:
- Identify the interval. Hint: They are not all sevenths.
Chopin[7], Etude, Op. 25, No. 5 – Vivace

Click here to watch the tutorial.
Solution
9.6 ENHARMONICALLY EQUIVALENT INTERVALS
Previously, we learned that the inversion of an augmented fourth is a diminished fifth. These two intervals also have another interesting characteristic. Play Example 9.6.1 on the piano. What do you notice?
Example 9.6.1. Augmented fourth and diminished fifth
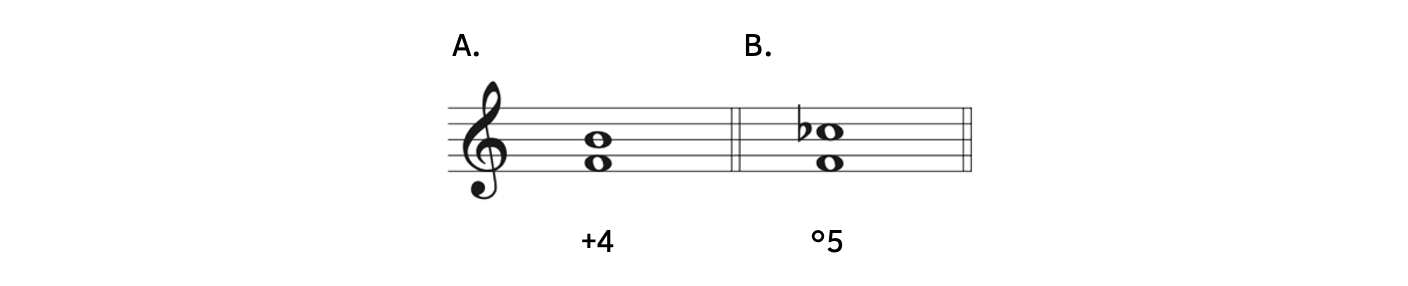
The augmented fourth sounds like the diminished fifth. Recall that when music sounds the same but is spelled differently, they are enharmonic equivalents. So far, we have learned about enharmonically equivalent notes (e.g., D![]() and E
and E![]() ) and enharmonically equivalent keys (e.g., F
) and enharmonically equivalent keys (e.g., F![]() major and G
major and G![]() major). We can also have enharmonically equivalent intervals (e.g., +4 and o5). Example 9.6.2 shows just a few examples of enharmonically equivalent intervals.
major). We can also have enharmonically equivalent intervals (e.g., +4 and o5). Example 9.6.2 shows just a few examples of enharmonically equivalent intervals.
Example 9.6.2. Enharmonically equivalent intervals

- Example 9.6.2A1: A minor third is enharmonically equivalent to an augmented second.
- Example 9.6.2A2: The augmented second can be spelled by writing an enharmonically equivalent top note.
- Example 9.6.2A3: The augmented second can be spelled by writing an enharmonically equivalent bottom note.
- Example 9.6.2B: A perfect fourth is enharmonically equivalent to an augmented third. By changing F to its enharmonically equivalent E
 , the interval changes from a perfect fourth to an augmented third.
, the interval changes from a perfect fourth to an augmented third. - Example 9.6.2C: A major sixth is enharmonically equivalent to a diminished seventh. By changing A
 to G
to G , the interval changes from a major sixth to a diminished seventh.
, the interval changes from a major sixth to a diminished seventh.
Although enharmonically equivalent intervals sound the same, it is important that you spell the interval correctly. Remember to always identify or write the interval number first.
Robert Schumann creates enharmonically equivalent intervals in Example 9.6.3.
Example 9.6.3. Enharmonically equivalent intervals: Schumann[8], Dichterliebe, Op. 48, No. 12, “Am leuchtenden Sommermorgen” (“On a Bright Summer Morning”)

In “Am leuchtenden Sommermogen,” Schumann switches the pianist’s part to sharps while the vocalist maintains flats. As a result, enharmonically equivalent intervals occur. Each interval is based on the bass clef’s lowest note.
- Example 9.6.3A:
- Example 9.6.3A1: The vocalist’s B
 creates a diminished fourth with the low F
creates a diminished fourth with the low F .
. - Example 9.6.3A2: At the same time, the pianist’s A
 forms a major third with the low F
forms a major third with the low F .
. - The diminished fourth and the major third are enharmonically equivalent intervals.
- Example 9.6.3A1: The vocalist’s B
- Example 9.6.3B:
- Example 9.6.3B1: The vocalist’s D
 creates a diminished sixth with the low F
creates a diminished sixth with the low F .
. - Example 9.6.3B2: Meanwhile, the pianist’s C
 forms a perfect fifth with the low F
forms a perfect fifth with the low F .
. - The diminished sixth and the perfect fifth are enharmonically equivalent intervals.
- Example 9.6.3B1: The vocalist’s D
- Example 9.6.3C:
- Example 9.6.3C1: The vocalist’s D
 creates a diminished octave with the low B.
creates a diminished octave with the low B. - Example 9.6.3C2: Meanwhile, the pianist’s C
 forms a major second with the low B.
forms a major second with the low B. - The diminished third and the major second are enharmonically equivalent intervals.
- Example 9.6.3C1: The vocalist’s D
- Example 9.6.3D:
- Example 9.6.3D1: The vocalist’s B
 creates a diminished ninth (or compound diminished second) with the low B.
creates a diminished ninth (or compound diminished second) with the low B. - Example 9.6.3D2: At the end of the bar, the pianist’s B forms a perfect octave with the low B.
- The diminished ninth and the perfect octave are enharmonically equivalent intervals.
- Example 9.6.3D1: The vocalist’s B
Why would Schumann write all these enharmonically equivalent intervals? Schumann did not accidentally use flats in the vocalist’s part and sharps in the piano’s part. Observe the lyrics: “Whisper and speak the flowers.” Schumann is able to convey uncertainty and confusion by combining flats and sharps while the vocalist sings about flowers speaking to him. While the piano part includes conventional perfect and major intervals, the vocalist’s part creates enharmonically equivalent diminished intervals.
Enharmonically Equivalent Intervals
Enharmonically equivalent intervals are intervals that sound the same but are spelled differently.
Practice 9.6. Finding Enharmonically Equivalent Intervals
Directions:
- Write an enharmonically equivalent interval for the given intervals. You can use the keyboard below to help you.

Click here to watch the tutorial.
Solution
9.7 TRITONE
In the last section, we learned that an augmented fourth and a diminished fifth are enharmonically equivalent intervals. These two intervals are also known as the tritone. Tritone, which gets its name from “three tones,” refers to the three whole steps between notes in an augmented fourth.
Example 9.7.1. Tritone: three whole steps

In Example 9.7.1, the square brackets represent whole steps. Because the inversion of an augmented fourth is a diminished fifth and because the two intervals are enharmonically equivalent, we also call the diminished fifth a tritone even though it is literally not made of three whole steps.
In addition to being interval inversions and enharmonically equivalent, the tritone has several other unique characteristics. We learned about all the intervals in a major scale and a natural minor scale when you based the intervals from the tonic.
Example 9.7.2. Intervals from tonic

Although these scales contain a variety of intervals, the minor second is missing. However, when we look at intervals between all possible pairs of notes of the scale (i.e., not only notes paired with tonic), we can find two minor seconds:
- In a C major, there is a minor second between E and F, and between B and C.
- In a C natural minor, there is a minor second between D and E-flat, and between G and A-flat.
When we tally all the intervals found between all combinations of notes in the major and natural minor scales, we get the following results.
Example 9.7.3. Number of intervals
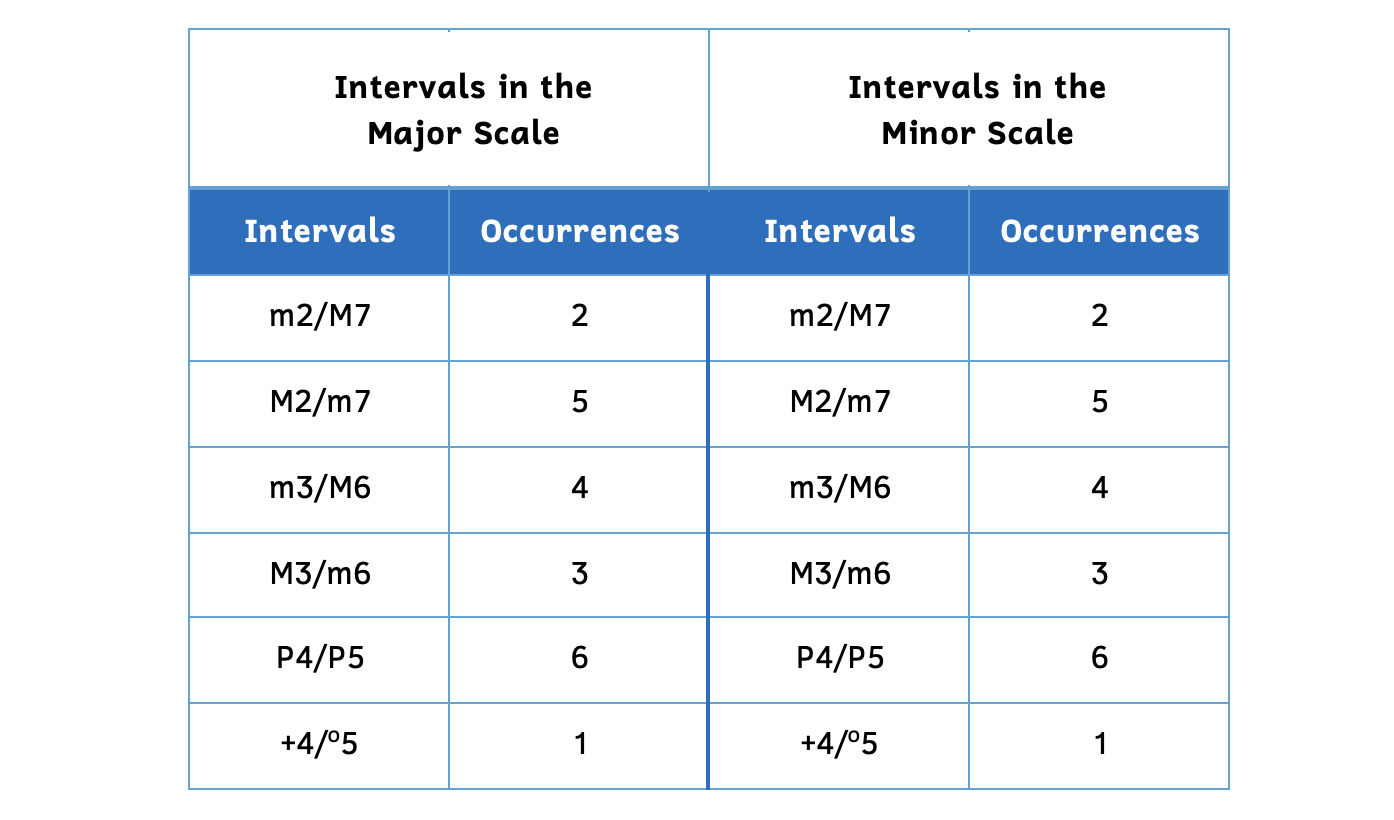
Notice that intervals are paired with their inversions. This is because although the distance from C up to B is a major seventh and the distance between its inversion (from B up to C) is a minor second, we do not count the interval between B and C twice. Therefore, it is only counted once in the m2/M7 category.
- There are two instances of minor seconds or major sevenths.
- In major, they occur between E/F and B/C.
- In minor, they occur between D/E-flat and G/A-flat.
- There are five instances of major seconds or minor sevenths.
- In major, they occur between C/D, D/E, F/G, G/A, and A/B.
- In minor, they occur between C/D, E-flat/F, F/G, A-flat/B-flat, and B-flat/C.
- There are four instances of minor thirds or major sixths.
- In major, they occur between D/F, E/G, A/C, and B/D (i.e., the all-white-key minor thirds).
- In minor, they occur between C/E-flat, D/F, F/A-flat, and G/B-flat.
- There are three instances of major thirds or minor sixths.
- In major, they occur between C/E, F/G, and G/B (i.e., the all-white-key major thirds).
- In minor, they occur between E-flat/G, A-flat/C, and B-flat/D.
- There are six instances of perfect fourths or perfect fifths.
- In major, they occur between C/F, D/G, E/A, G/C, A/D, and B/E. This is why the accidentals match for all perfect fourths and fifths except for F/B.
- In minor, they occur between C/F, D/G, E-flat/A-flat, F/B-flat, G/C, and B-flat/E-flat.
- There is only one instance of an augmented fourth or diminished fifth in major and one instance in minor.
- In major, it occurs between F/B.
- In minor, it occurs between A-flat/D.
This means that of all the intervals in any major or minor scale, the tritone is the only interval that only occurs once. Example 9.7.4 illustrates where the tritone appears in both the major and natural minor scales.
Example 9.7.4. Tritones in major and natural minor scales

Since there is only one tritone found in the major scale, and one tritone found in the natural minor scale, the tritone plays an important role as a key-defining interval. Let’s break down this statement.
- Example 9.7.4A: In major, the unique tritone is between
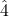 and
and 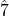 .
.
- In C major, the tritone is between F and B.
- This means that there is no other major scale that has both F and B, because the pair is unique only to C major.
- If there is one sharp in a key signature, it is F-sharp; if there is one flat in a key signature, it is B-flat. Since C major has no sharps or flats, it is the only major key that has both F and B.
- Example 9.7.4B: In minor, the unique tritone is between
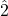 and
and 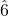 .
.
- In C minor, the tritone is between D and A-flat.
- This means that there is no other minor scale that has both D and A-flat, because the pair is unique only to C minor.
- The order of flats is B-flat–-E-flat-–A-flat-–D-flat-–G-flat-–C-flat-–F-flat. If there are two flats, neither D nor A is flatted; if there are four flats, both D and A are flatted. Therefore, only C minor, which has three flats, has both D and A-flat.
Another important characteristic of the tritone is that the two notes that make up a tritone are tendency tones: notes that have a strong desire to move a certain way. Because there are half steps on either side of the tritone and half steps are twice as small as whole steps, tension creates the desire for notes to move in the direction of the half steps.
Example 9.7.5. Tendency tones in tritones (augmented fourth)
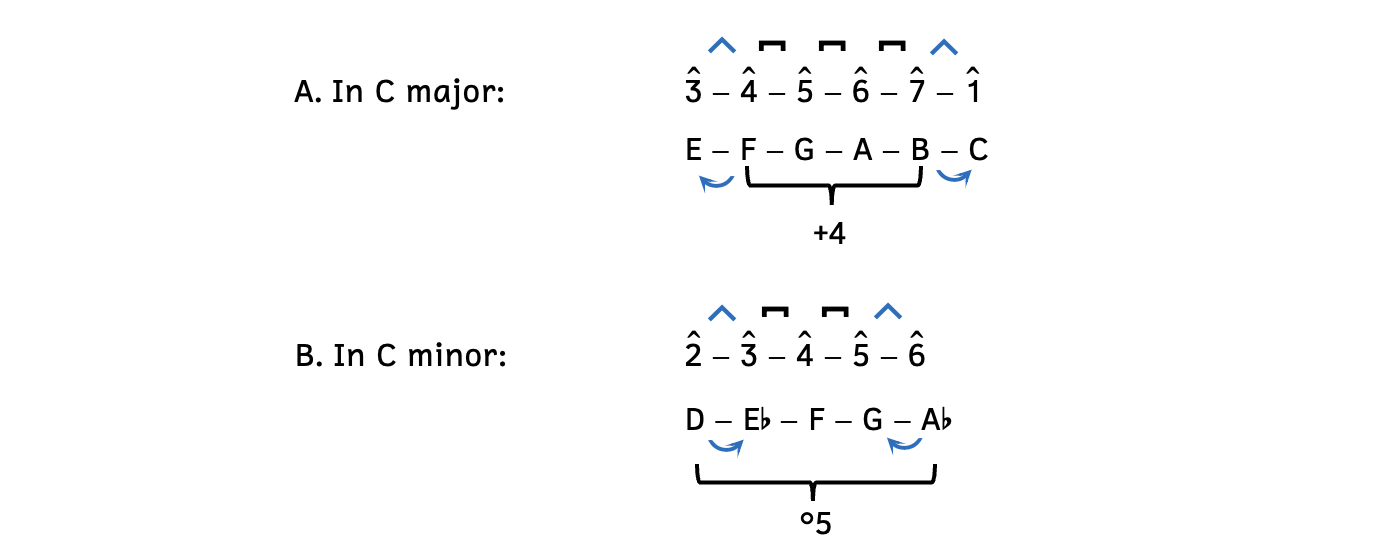
Half steps surrounding the tritone (i.e., the tendency tones) in both C major and C minor are represented by blue carets.
- Example 9.7.5A: In major,
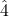 wants to resolve down to
wants to resolve down to 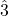 , while
, while  wants to resolve up to
wants to resolve up to 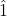 .
.
- Recall that
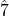 is also known as the leading tone, meaning that it leads to tonic.
is also known as the leading tone, meaning that it leads to tonic. - In C major, F (
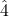 ) wants to resolve down to E (
) wants to resolve down to E (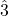 ), and B (
), and B (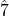 ) wants to resolve up to C (
) wants to resolve up to C ( ).
).
- Recall that
- Example 9.7.5B: In minor,
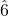 wants to resolve down to
wants to resolve down to 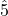 , while
, while 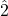 wants to resolve up to
wants to resolve up to 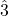 .
.
- In C minor, A-flat (
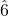 ) wants to resolve down to G (
) wants to resolve down to G (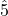 ), and D (
), and D (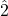 ) wants to resolve up to E-flat (
) wants to resolve up to E-flat (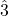 ).
).
- In C minor, A-flat (
As a result of these tendency tones, we see that a tritone in the form of an augmented fourth wants to resolve outward (Example 9.7.5A), while a tritone in the form of a diminished fifth wants to resolve inward (Example 9.7.5B).
Recall that when we analyze a piece in minor, it will usually use the harmonic minor or melodic minor scale, where ![]() is raised. This changes
is raised. This changes ![]() from the subtonic to the leading tone. As a result, another tritone is often formed in minor.
from the subtonic to the leading tone. As a result, another tritone is often formed in minor.
Example 9.7.6. Additional tritones in minor

- Example 9.7.6A: When the subtonic is raised to become the leading tone, there is a new tritone between
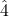 and
and 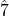 .
. - Example 9.7.6B: Similarly, there is also a new tritone between
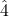 and
and 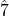 in the ascending melodic minor scale. Remember that the descending melodic minor scale returns back to the natural minor scale.
in the ascending melodic minor scale. Remember that the descending melodic minor scale returns back to the natural minor scale.
In both major and minor, the tendency tones in the tritone between ![]() and
and ![]() (raised
(raised ![]() in minor) play a powerful role. This tritone is so powerful that although there is a whole step (as opposed to a half step) between
in minor) play a powerful role. This tritone is so powerful that although there is a whole step (as opposed to a half step) between ![]() and
and ![]() in minor, the desire for
in minor, the desire for ![]() to resolve down to
to resolve down to ![]() still exists.
still exists.
Example 9.7.7. Resolving ![]() and
and ![]() /raised
/raised ![]() in major and minor
in major and minor
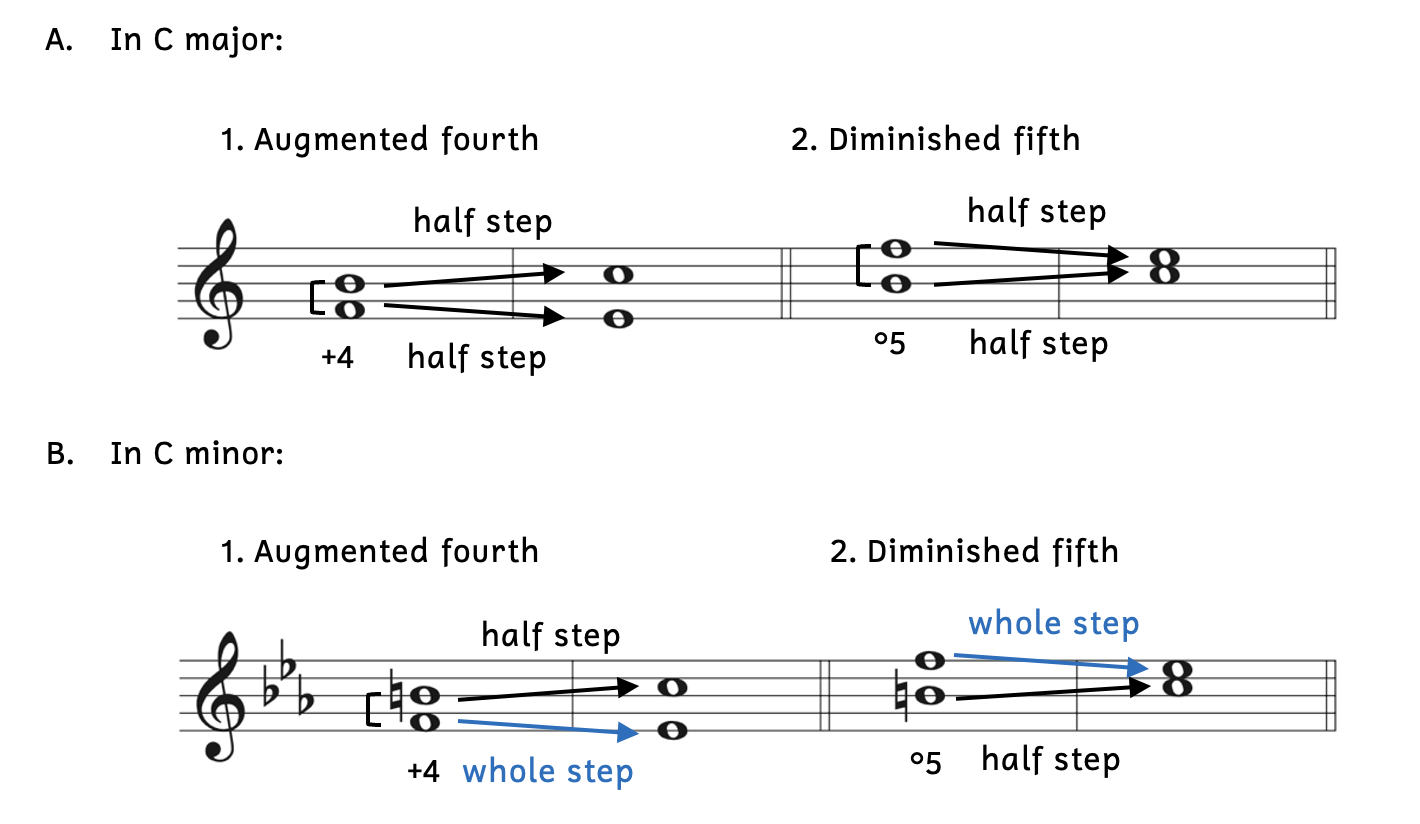
- Example 9.7.7A: The members of the tritone in C major are F and B. In C major,
 (B) resolves up by half step to
(B) resolves up by half step to 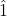 (C) and
(C) and 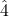 (F) resolves down by half step to
(F) resolves down by half step to 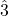 (E).
(E).
- A1: The augmented fourth resolves outward by half step in both notes.
- A2: The diminished fifth resolves inward by half step in both notes.
- Example 9.7.7B: In C minor, a tritone is formed between F and B-natural with the raised
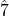 (B-natural). In C minor, raised
(B-natural). In C minor, raised 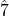 (B-natural) resolves up by half step to
(B-natural) resolves up by half step to 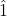 (C) and
(C) and 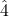 (F) resolves down by whole step to
(F) resolves down by whole step to 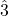 (E-flat). There is no longer a half step between
(E-flat). There is no longer a half step between 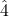 (F) and
(F) and 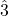 (E-flat) because in minor,
(E-flat) because in minor, 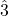 is lowered from mi to me. This forms a whole step between
is lowered from mi to me. This forms a whole step between 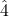 and
and 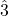 . However, because the tritone between
. However, because the tritone between 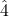 (fa) and
(fa) and 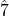 (ti) is so strong,
(ti) is so strong, 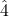 (fa) still wants to resolve down to
(fa) still wants to resolve down to 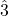 (me).
(me).
- B1: The augmented fourth still resolves outward by step, but there is a whole step between
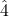 (F) and
(F) and 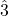 (E-flat).
(E-flat). - B2: The diminished fifth still resolves inward by step, but again, there is a whole step between
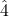 (F) and
(F) and 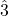 (E-flat).
(E-flat).
- B1: The augmented fourth still resolves outward by step, but there is a whole step between
In Example 9.7.8, we see how Beethoven resolves tritones.
Example 9.7.8. Resolved tritones: Beethoven, Piano Sonata No. 8 in C Minor, Op. 13, (“Pathètique”), i – Grave. Allegro di molto e con brio

- In the first system, there are three tritones. The pitches F-sharp and C form a tritone.
- When F-sharp is below C, the tritone is a diminished fifth and when C is below F-sharp, the tritone is an augmented fourth.
- Since F-sharp and C form a diminished fifth, we know that F-sharp is
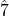 and C is
and C is 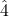 . Based on how these tendency tones resolve, the first system is in the key of G major. Indeed, each tritone resolves to G and B, which are
. Based on how these tendency tones resolve, the first system is in the key of G major. Indeed, each tritone resolves to G and B, which are 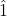 and
and 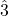 in G major.
in G major.
- In the second system, there are also three tritones. The pitches D-flat and G form a tritone.
- When D-flat is below G, the tritone is an augmented fourth and when G is below D-flat, the tritone is a diminished fifth.
- Since D-flat and G form an augmented fourth, we know that D-flat is
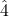 and G is
and G is 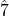 . Based on how these tendency tones resolve, the second system is in the key of A-flat major. Indeed, each tritone resolves to A-flat and C, which are
. Based on how these tendency tones resolve, the second system is in the key of A-flat major. Indeed, each tritone resolves to A-flat and C, which are 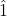 and
and 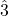 in A-flat major.
in A-flat major.
A simple way to identify the key of the example is to look for the leading tone of the tritone. The leading tone usually resolves up to tonic, which tells you the name of the key.
Tritone
The tritone is an important interval in both major and minor keys. It is a unique key-defining interval and both notes are tendency tones.
- In major keys, the tritone is between
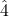 and
and 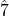
- In minor keys, the tritone is
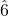 and
and 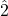 and with the raised leading tone, between
and with the raised leading tone, between 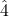 and
and 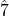 .
.
Practice 9.7A
Directions:
- In part A, identify the tritone as a diminished fifth (o5) or an augmented fourth (+4).
- On the staff, draw arrows to indicate whether the notes of the tritone resolve up or down.
- In the blank staff, resolve the tritone by moving each note by a minor second.
- In part B, identify the major key to which the tritone belongs. Hint: The leading tone (
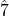 ) resolves up by step to the tonic (
) resolves up by step to the tonic ( ), which is also the name of the key.
), which is also the name of the key.

Click here to watch the tutorial.
Practice 9.7B
Directions: In Example 9.7.8, we saw how Beethoven utilizes and resolves tritones. Later, Beethoven makes the tritones more obvious, which is shown below.
- In the passage below, circle and label all tritones.
- Draw arrows to show how members of the tritone resolve.
- Identify in what major key the excerpt is. Hint:
 resolves up to the tonic.
resolves up to the tonic.
Beethoven, Piano Sonata No. 8 in C Minor, Op. 13, (“Pathètique”), i – Grave. Allegro di molto e con brio

Click here to watch the tutorial.
9.8 CONSONANCE AND DISSONANCE
In Section 9.6, we learned about enharmonically equivalent intervals: intervals that sound the same but are spelled differently. Based on how intervals are spelled, they can sound stable or unstable. Compare Examples 9.8.1A and B.
Example 9.8.1. Enharmonically equivalent intervals in context
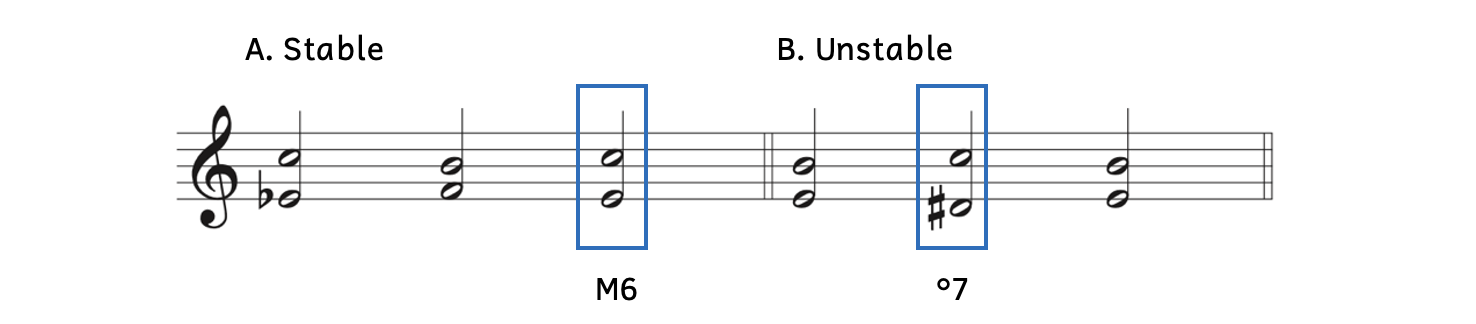
- Example 9.8.1A: Listen to the boxed interval of a major sixth. There is a sense of stability in this interval, meaning that we could end with this interval.
- Example 9.8.1B: Now play only the first two intervals of this example. Do you hear how unstable the diminished seventh sounds? After the diminished seventh, we long to hear the following interval, which is stable. Now play all three chords—did you feel the sense of resolution after the third chord?
The major sixth in Example 9.8.1A and the diminished seventh in Example 9.8.1B are enharmonically equivalent intervals. However, a the major sixth sounded stable while the diminished seventh sounded unstable.
When an interval sounds stable, it is called a consonant interval; when an interval sounds unstable, it is called a dissonant interval. Within the consonant intervals, there are two types: perfect consonances and imperfect consonances. The perfect consonances are the most stable. Historically, music for two voices could only begin and end with perfect consonances.
You can think about the stability and instability of consonant and dissonant intervals by visualizing them with pyramids.
Example 9.8.2. Stability and instability

- Example 9.8.2A: Perfect consonances are very stable. Imagine having a pyramid shaped like Example 9.8.2A with a large base sitting on the table: It would be difficult to knock over.
- Example 9.8.2B: Imperfect consonances are also stable, but less stable than perfect consonances. If you had a pyramid shaped like Example 9.8.2B with a narrow base, it could stand on its own, but would be easy to accidentally knock over.
- Example 9.8.2C: Dissonances are unstable. If you had a pyramid shaped like Example 9.8.2C, the pyramid could not stand upright on its tip. As you will later see, dissonances must be treated with great care since they are so unstable.
The table below shows the most common intervals and whether they are a perfect consonance (PC), imperfect consonance (IC), or dissonance (D).
Example 9.8.3. Consonance and dissonance table
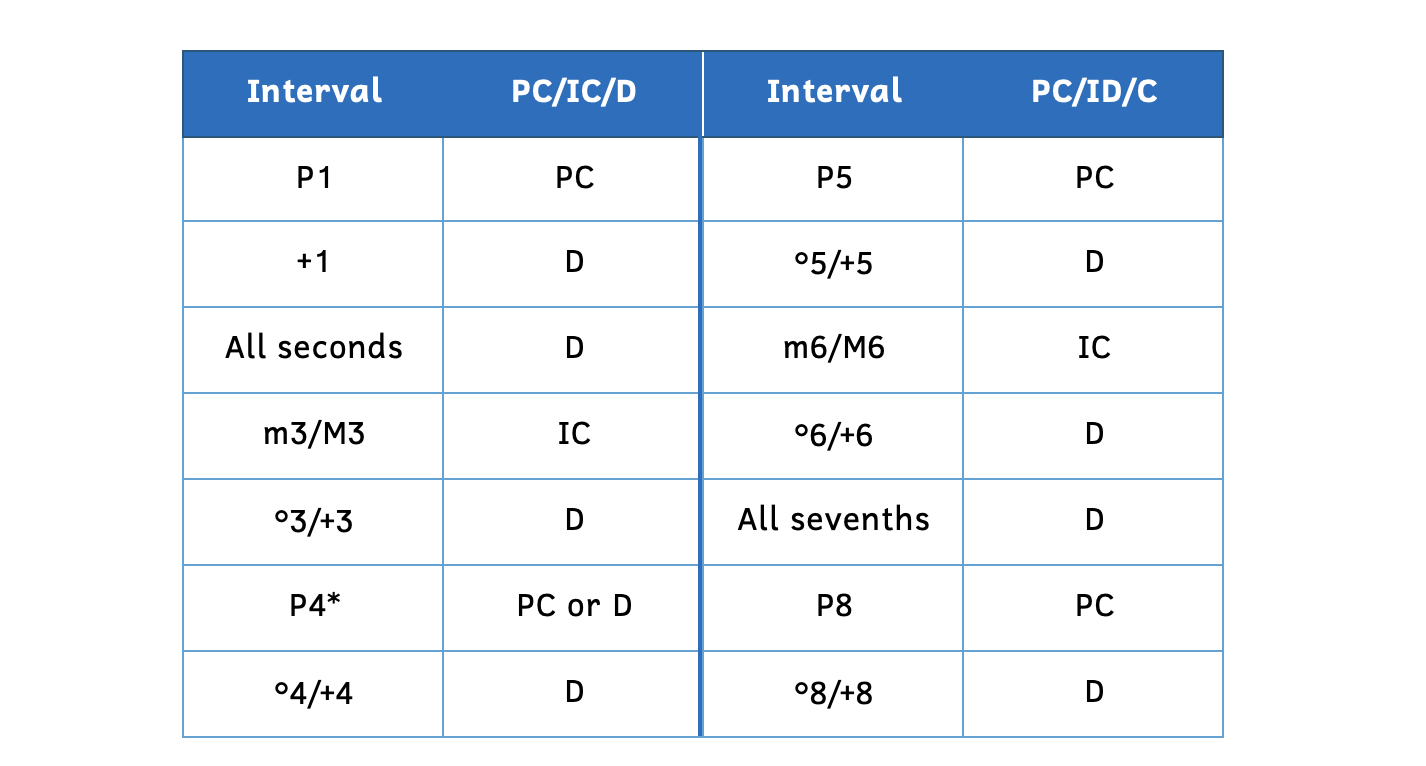
- There are a few statements that can help you remember the dissonant intervals:
- All seconds and sevenths are dissonant.
- All diminished and augmented intervals are dissonant.
- Sometimes the perfect fourth is dissonant.
- Only the perfect intervals are perfect consonances (except the perfect fourth sometimes).
- This leaves the minor third, major third, minor sixth, and major sixth as imperfect consonances.
You may have noticed that the unison does not have a diminished version. This is because since intervals are based on the lower note, anything other that a perfect unison would be an augmented unison.
The perfect fourth can be a dissonance or a perfect consonance.[9]
Example 9.8.4. Perfect fourth

- Sometimes the perfect fourth is dissonant.
- Example 9.8.4A: When there are only two notes and a perfect fourth is a harmonic interval, then the perfect fourth is dissonant.
- Example 9.8.4B: When there are more than two notes and a perfect fourth is a harmonic interval with the lowest note, then the perfect fourth is dissonant.
- Sometimes the perfect fourth is consonant.
- Example 9.8.4C: When there are more than two notes and a perfect fourth is a harmonic interval but does not include the lowest note, then the perfect fourth is a perfect consonance.
- Example 9.8.4D: When the perfect fourth is a melodic interval, it is a perfect consonance.
Composers often use a variety of consonant and dissonant intervals between the highest part and the lowest part. Example 9.8.5D illustrates the diversity of consonances and dissonances in a Szymanowska march.
Example 9.8.5. Consonant and dissonant intervals: Szymanowska[10], March No. 1 in B-flat Major

The majority of intervals Szymanowska uses are consonant. However, the consonances are split between perfect consonances and imperfect consonances. Dissonant intervals are sprinkled throughout, but there are never two dissonances in a row.
Perfect Consonances (PC), Imperfect Consonances (IC), and Dissonances (D)
Intervals are categorized by how stable (consonant) or unstable (dissonant) they are. Within the consonant intervals, there are perfect consonances and imperfect consonances.
- All seconds and sevenths are dissonant.
- All diminished and augmented intervals are dissonant.
- Imperfect consonances include the m3, M3, m6, and M6.
- All perfect intervals are perfect consonances (except sometimes the P4).
- The P4 can be a perfect consonance or a dissonance, depending on the situation.
Practice 9.8A
Directions:
- Fill in the table: perfect consonance (PC), imperfect consonance (IC), or dissonance (D).
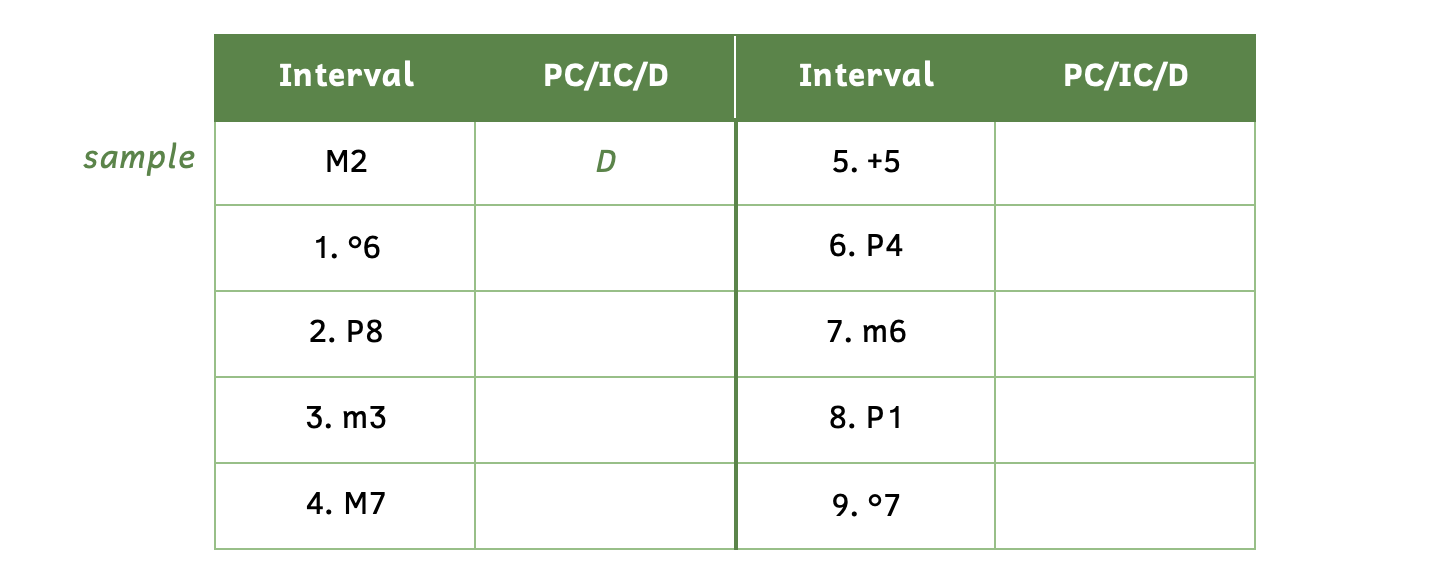
Click here to watch the tutorial.
Solution
Practice 9.8B
Directions:
- Identify all intervals between the highest and lowest sounding parts in the given blanks.
- Below the intervals, write whether the interval is a perfect consonance (PC), imperfect consonance (IC), or dissonance (D).
Szymanowska, March No. 5 in B-flat Major

Click here to watch the tutorial.
Solution
9.9 TRANSPOSITION: INTERVALLIC
Recall that transposition refers to when you change all notes and rests equally by the same proportion. In Chapter 4, we learned about melodic transposition, when we rewrote music in a different key by using the same scale degrees with a different key signature. Intervallic transposition is similar to melodic transposition because it will result in a melody in a different key. However, the method to get the same result is different. With intervallic transposition, you transpose each note up or down by the same interval.
There are two methods to intervallic transposition:
- Method #1: Identify the intervals between each note and apply the same intervals to the transposed melody. Recall that the way that music rises and falls is called melodic contour. You must be precise with melodic contour.
- Method #2: Identify the interval between the first note of the melody and the first note of the transposed melody. Transpose the new melody by applying that interval to each note.
We will apply both methods to the melody in Example 9.9.1.
Example 9.9.1. Melody

For Method #1, apply the same interval between notes to the new starting pitches.
Example 9.9.2. Intervallic transposition using Method #1

- Example 9.9.2A: Beginning on D, the same intervals are applied.
- A major third above D is F-sharp, so a sharp must be added.
- Example 9.9.2B: Beginning on E-flat, the same intervals are applied.
- A minor third above G is B-flat, so a flat must be added.
Method #2 involves transposing each note of the melody by the same interval as the interval between the first note of the original melody and new melody.
Example 9.9.3. Intervallic transposition by Method #2

- Example 9.9.3A: Because the interval from B-flat4 to D5 is an ascending major third, write every note a major third higher for Example 9.9.3A2.
- Example 9.9.3B: Because the interval from B-flat4 to E-flat4 is a descending perfect fifth, write every note a perfect fifth lower for Example 9.9.3B2.
Example 9.9.4 illustrates intervallic transposition in a fugue by Clara Wieck Schumann. A fugue is a strict compositional technique in which the opening melody (called the subject) repeats throughout the work at specific intervals (called the answer).
Example 9.9.4. Intervallic transposition: Wieck Schumann[11], Three Preludes and Fugues, Op. 16, Fugue No. 2

- The fugue begins with the melody (called the subject) in the lowest voice.
- In measure 4, a second voice (called the answer) enters with the melody. You can tell a second voice entered because of the stem directions. Beginning in measure 4, the stem direction of the first voice points down while the stem direction of the second voice points up.
Because the intervallic transposition may be difficult to see, Examples 9.9.5 and 9.9.6 show the subject and answer above one another. Example 9.9.5 uses Method #1.
Example 9.9.5. Intervallic transposition Method #1: Wieck Schumann, Three Preludes and Fugues, Op. 16, Fugue No. 2

Example 9.9.5 shows the intervals between pitches in the subject, then applies the same intervals in the answer. Notice that the melodic contour is the same. Alternatively, you can use Method #2 and complete intervallic transposition by rewriting every note in the answer a perfect fifth higher (Example 9.9.6).
Example 9.9.6. Intervallic transposition Method #2: Wieck Schumann, Three Preludes and Fugues, Op. 16, Fugue No. 2

In Example 9.9.6, the answer begins a perfect fifth higher than the subject. Applying Method #2, each note from the answer is then written a perfect fifth higher than each note of the subject.
Listen to Example 9.9.4 again and how the answer enters while the first voice is still playing. Fugues have a polyphonic texture, meaning that there is more than one voice with the melody at the same time. It may seem that voice entries would be difficult to hear but composers intentionally write distinctive openings to their fugal subjects that can easily be distinguished.
Intervallic Transposition
Intervallic transposition is when you transpose each note by the same interval. There are two methods for intervallic transposition.
- Method #1: Transpose each note by the melodic interval between notes. Be sure to maintain the melodic contour.
- Method #2: Find the interval between the first note of the original melody and the first note of the new melody. Write the new melody using the same interval.
Practice 9.9A
Directions:
- For #1, use Method #1. Write the direction and interval (e.g., ascending M3) between each note. For #1B, copy the pattern to transpose the melody beginning on the given note.
- For #2, use Method #2. Figure out the interval between the first note of #2A and the first note of #2B. Then transpose each note by that interval for #2B.
- Write the melody in the new key and add all appropriate musical symbols.

Click here to watch the tutorial.
Practice 9.9B
Directions:
- In measures 5-8, transpose the second voice (answer) above the first voice (subject) by a perfect fifth. The answer begins on the downbeat of measure 5 and downbeats have been given to you as a guide.
Wieck Schumann, Three Preludes and Fugues, Op. 16, Fugue No. 3.

9.10 ANALYSIS: BRAHMS, SYMPHONY NO. 4
Intervals can play an important role in some pieces. Look at Example 9.10.1, which is the opening melody of Brahms’s Fourth Symphony.
Example 9.10.1. Brahms[12], Symphony No. 4 in E Minor, Op. 98, i – Allegro non troppo

The violins begin with this lulling melody, with ascending and descending pairs of notes. When we analyze the pairs of notes, we see that the intervals are a descending major third, ascending minor sixth, descending minor third, and ascending minor sixth. What relationship do thirds and sixths have? They are interval inversions.
Since sixths are the inversion of thirds, we can invert the sixths to create this reinterpretation of the opening melody:
Example 9.10.2. Melody with inversions

https://tamucc.pressbooks.pub/app/uploads/sites/2/2023/09/Screenshot-2023-09-11-at-4.07.06-AM.png
In Example 9.10.2, the two ascending sixths are inverted to become descending thirds. By inverting the sixths into thirds, we see a pattern of four pairs of descending thirds.
What about the relationship between the pairs? If we look at each note on either side of each quarter rest, we see there is the potential for more thirds.
Example 9.10.3. Melody as thirds

Example 9.10.3 includes the thirds between the pairs of notes. Amazingly, the opening of Brahms’s Fourth Symphony is simply made of descending thirds. If Brahms wrote the opening like in Example 9.10.3, it would be quite boring. However, with the use of inversions, he created a beautiful melody that did not sound like a chain of descending thirds.
The descending thirds return in the fourth movement, almost in a humorously obvious way (Example 9.10.4).
Example 9.10.4. Descending thirds: Brahms, Symphony No. 4 in E Minor, Op. 98,

The excerpt begins with six notes moving in descending thirds.
- Beginning on beat 2, the first and second violins play descending thirds an octave apart. The first violins start on E6 and the second violins start on E5.
- Beginning on the downbeat, the cellos and double basses play descending thirds an octave apart. (The double bass sounds an octave lower than what is written.) The cellos start on E4 and the double basses start on E3.
- This means that there are four parts in four octaves playing the same descending thirds, but two instruments begin one beat later, creating a canon. A canon is a type of polyphonic texture in which the same melody repeats in another voice, while overlapping the first voice.
After each instrument plays B, there is a large ascending leap, seemingly breaking the chain of descending thirds.
- Between beats 1 and 2 of measure 243, the first and second violins leap up from B4 and B3 up to G6 and G5.
- Across the bar line between measures 242 and 243, the cellos and basses leap up from B2 and B1 to G4 and G3.
Upon closer inspection, the chain of descending thirds is not broken, as the leap from B up to G is a compound sixth: the inversion of a third (Example 9.10.5).
Example 9.10.5. Interval inversions

- Example 9.10.5A: The circled interval is extremely large. It is an ascending compound minor sixth.
- Example 9.10.5B: When inverting the interval, the higher note becomes the lower note. Here G6 is moved down two octaves so that it is now below B4. Its inversion of a third becomes clear when put in context with the previous notes.
Just as Brahms had done in the opening of the first movement, he uses a series of descending thirds near the end of the finale. What makes the thirds in the fourth movement humorous is how blatantly Brahms exposes the descending thirds. While they are quite hidden in the opening, they are forte and in four octaves in the finale. One can imagine that if the strings did not have an issue with range, they would have only played descending thirds without having to use any interval inversions. As you start listening to and analyzing music, finding compositional devices can be a delightful surprise.
SUMMARY
-
-
- When you make a perfect or major interval a half step larger, it becomes augmented. When you make a perfect or minor interval a half step smaller, it becomes diminished. [9.1]
- Compound intervals are intervals larger than an octave. The exceptions are the ninth and tenth, since they are fairly common. [9.2]
- When you invert an interval, the bottom note becomes the top note and vice versa. [9.3]
- The inversion of perfect is perfect; the inversion of major is minor (and vice versa); and the inversion of diminished is augmented (and vice versa).
- The inversion of interval numbers adds up to nine.
- When writing intervals below a given note, it may be helpful to first write the interval inversion above to find your answer. [9.4]
- The shortcut for sevenths is to use the inversion to find the quality of the seventh. A minor second is a diatonic half step and a major second is a diatonic whole step. [9.5]
- Enharmonically equivalent intervals are intervals that sound the same but are spelled differently. [9.6]
- The tritone is a unique key-defining interval that is either an augmented fourth or a diminished fifth. [9.7]
- Consonant intervals are stable while dissonant intervals are unstable. [9.8]
- Perfect consonances include the P1, P4 (sometimes), P5, and P8.
- Imperfect consonances include the m3, M3, m6, and M6.
- All other intervals are dissonances. The perfect fourth is sometimes dissonant.
- Intervallic transposition is when you transpose each note by the same interval. [9.9]
- Brahms’s Fourth Symphony begins with a descending third, which returns through the movement and entire piece. [9.10]
-
TERMS
-
-
- answer
- augmented interval (+)
- canon
- compound interval
- consonant interval
- diminished interval (o)
- dissonant interval
- enharmonically equivalent intervals
- fugue
- imperfect consonance
- interval inversion
- intervallic transposition
- perfect consonance
- polyphony (polyphonic texture)
- simple interval
- subject
- tendency tones
- tritone
-
- Marie Rouband de Cournand (1822-1917) was a French composer and pianist. ↵
- Ethel Smyth (1858-1944) was an English composer. ↵
- Alexander Scriabin (1872-1915) was a Russian composer and pianist. ↵
- Barbara Strozzi (1619-1677) was an Italian composer and singer. ↵
- Ann Mounsey (1793-1867) was an English composer. ↵
- Ludwig van Beethoven (1770-1827) was a German composer. ↵
- Frédéric Chopin (1810-1849) was a Polish composer and pianist. ↵
- Robert Schumann (1810-1856) was a German composer and music critic. ↵
- Later, when we learn about chords, the perfect fourth as a dissonance or a perfect consonance will be applied in context. ↵
- Maria Szymanowska (1789-1831) was a Polish composer and pianist. ↵
- Clara Wieck Schumann (1819-1896) was a German composer and pianist. ↵
- Johannes Brahms (1833-1897) was a German composer. ↵
Interval quality when a perfect interval or minor interval is reduced by a half step while maintaining the interval number.
Interval quality when a perfect interval or major interval is increased by a half step while maintaining the interval number.
Intervals an octave or smaller.
Intervals a ninth or larger.
When the bottom note of an interval becomes the top note (or vice versa).
Intervals that sound the same but are spelled differently.
Literally "three (whole) steps"; interval of an augmented fourth (also a diminished fifth).
Notes that have a strong desire to move in a specific direction.
Stable-sounding interval. Two types: perfect consonances and imperfect consonances.
Unstable-sounding interval. Includes all seconds, sevenths, diminished, and augmented intervals.
Type of consonance that is most stable; includes the perfect unison, perfect fifth, perfect octave, and sometimes the perfect fourth.
Less stable than perfect consonances; includes major and minor thirds and sixths.
Changing all pitches by the same proportion; when you write or perform the same melody in a different key.
Transposing by using intervals (as opposed to key signatures).
The direction the melody ascends or descends.
Strict compositional technique in which the opening melody (called the subject) recurs throughout the work at different intervals. The second appearance of the melody is called the answer.
Opening melody of a fugue.
Second appearance of the melody of a fugue that occurs at a perfect fifth away from the subject (first appearance of the melody).
Texture of music in which multiple melodies occur simultaneously.
Type of polyphonic texture in which the same melody repeats in another voice, while overlapping the first voice.