Now that you are familiar with beats and meters within simple and compound meters, we will learn about less familiar rhythms and meters.

7.1  SYNCOPATION

In Chapters 3 and 5, we learned that there can be two, three, or four beats per measure. Although note values differ, the pattern of strong and weak beats is the same for simple and compound meters.

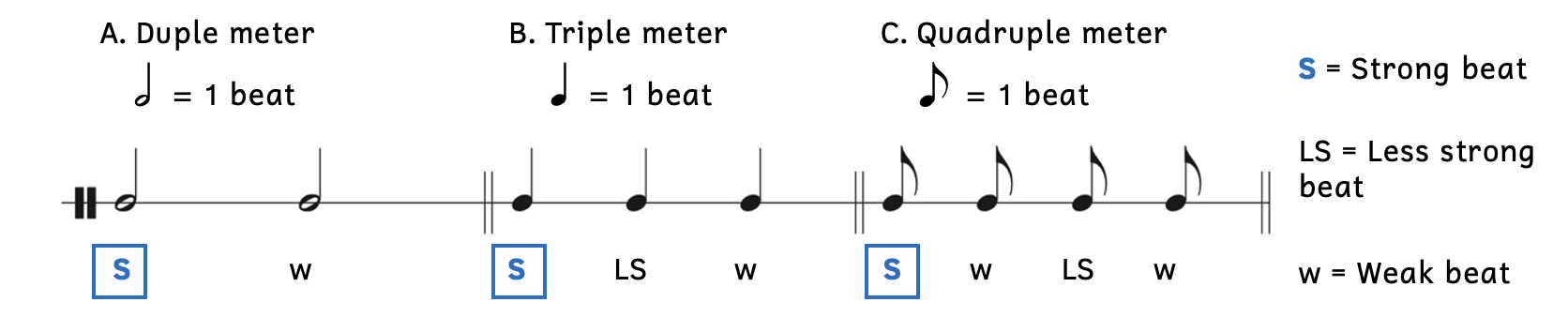
Example 7.1.1. Weighted beats in simple meters

Example 7.1.2. Weighted beats in compound meters

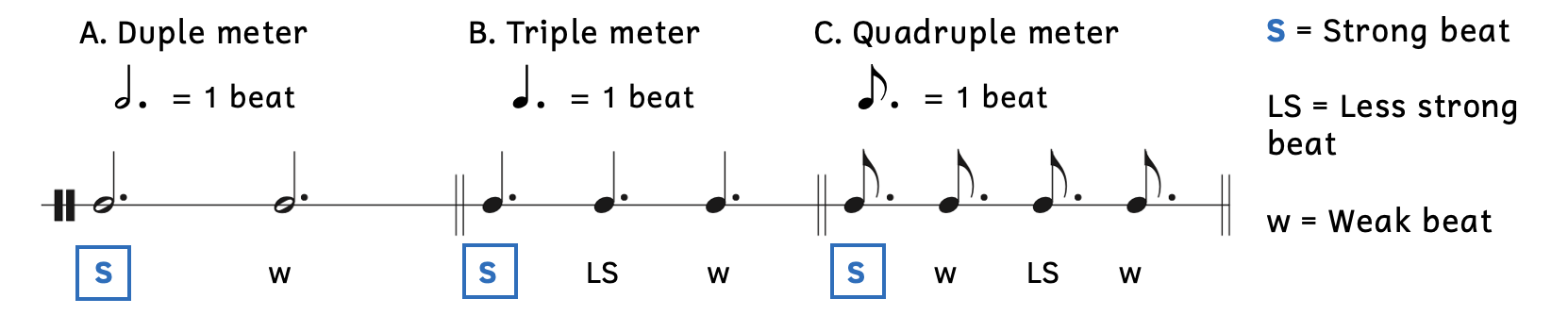
• In Examples 7.1.1 and 7.1.2, the downbeats are the strongest beats and are marked by the blue S’s in boxes.
• The next strongest beats vary.
  • In triple meters, beat 2 is less strong than the downbeat but stronger than beat 3.
  • In quadruple meters, beat 3 is less strong than the downbeat but stronger than beats 2 and 4.
• In each example, the last beat is a weak beat.

Sometimes composers will purposefully make naturally weaker beats stronger by placing more emphasis on them. When this occurs, it is called syncopation. John Philip Sousa achieves syncopations by two different methods in Example 7.1.3.

Example 7.1.3. Syncopation: Sousa^[1]: “Washington Post March”

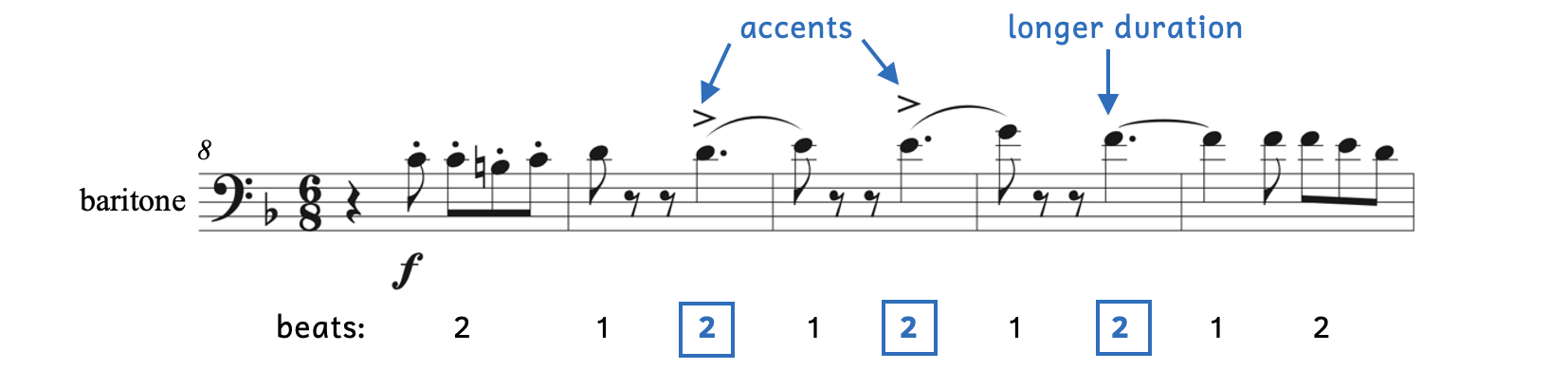
• The blue beats in boxes below Example 7.1.3. show syncopations.
• The first examples of syncopation are due to the accent markings. These accents force beat 2 to be stronger than the downbeat.
• The last example of syncopation is due to the longer duration tied into the next downbeat. Since there is no new sound occurring on the following downbeat, the sound that occurs on beat 2 is stronger.

Although Example 7.1.3 is not the start of the piece, the time signature has been added for convenience. Because this chapter covers less common rhythm and meters, every example in this chapter will include a time signature.

Syncopations are not simply one appearance of an accent. Rather, as in Examples 7.1.3, there must be accents on at least two regular occurrences in a row.  Now look at Example 7.1.4, which shows an accent on a weak beat that is not syncopation.

Example 7.1.4. Not a syncopation: Haydn^[2], Symphony No. 94, (“Surprise”), ii – Andante

In this piano reduction of Haydn’s “Surprise” Symphony (Example 7.1.4), a seemingly random fortissimo appears after almost sixteen bars of piano and pianissimo. The music then humorously returns to piano. No matter how accented this beat is, it is not considered a syncopation because there is no sense of regularity.

Example 7.1.5 does include syncopations because accents return at least two times.

Example 7.1.5. Syncopations: Guerreiro^[3], Bôas Festas, Op. 12

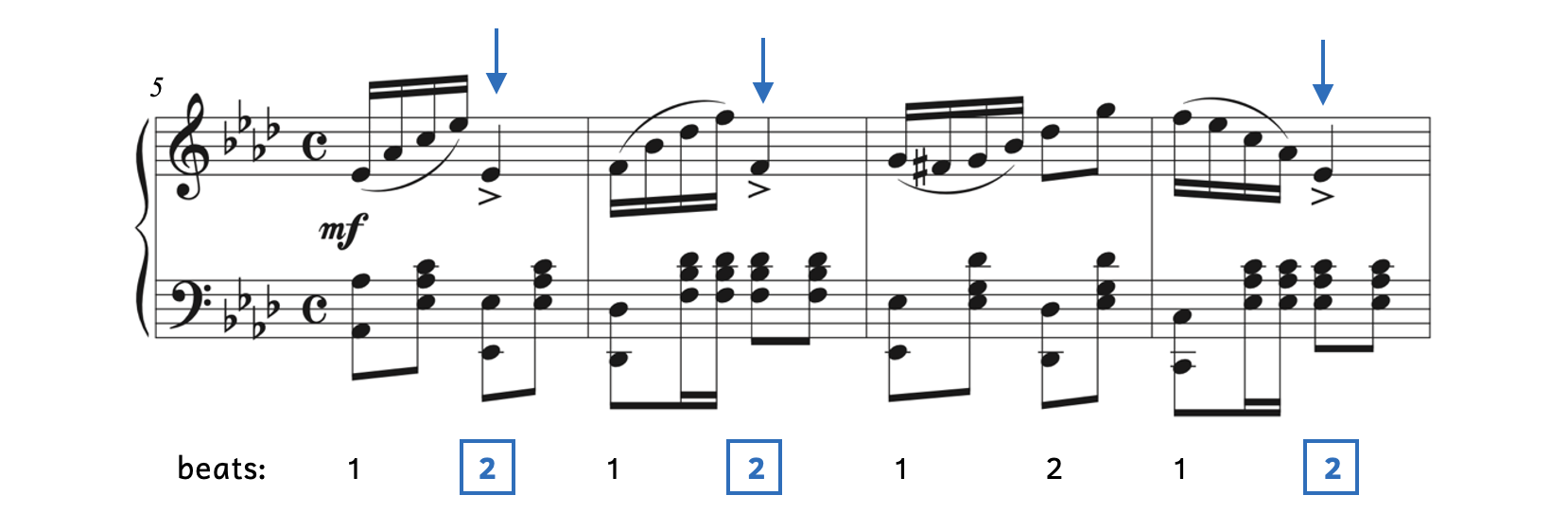
Several characteristics contribute to the syncopations in Example 7.1.5.

• There are accent marks on beat 2 of the treble clef in measures 5, 6, and 8.
• The quarter note’s longer duration of the accented notes also places emphasis on beat 2.
• The accents occur three times in the four measures of Example 7.1.5. If the accent only occurred once, it would not be an example of syncopation.

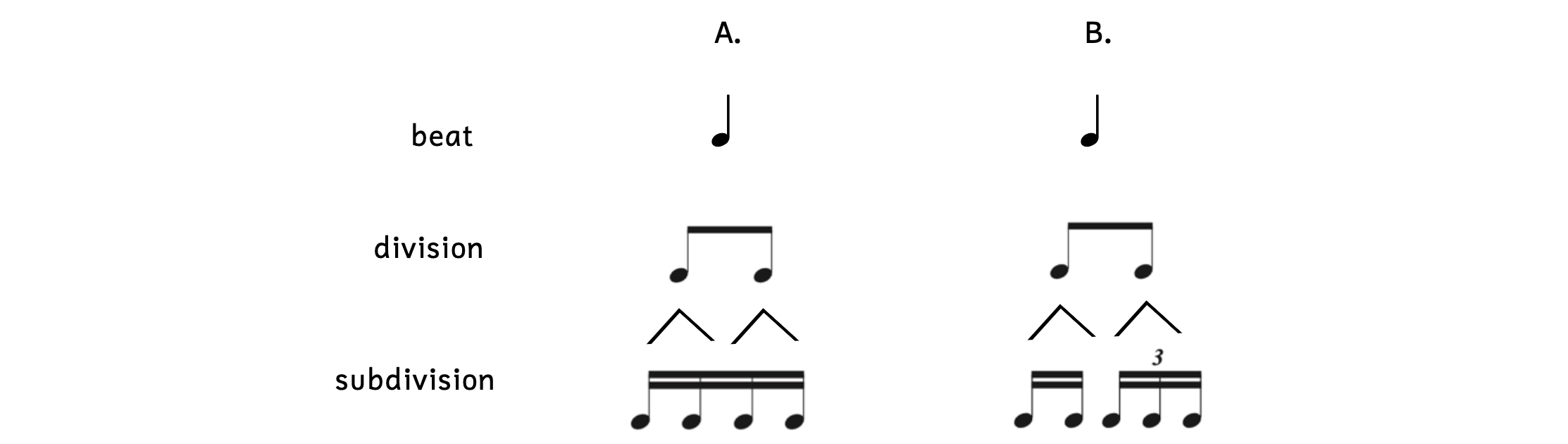
There can also be syncopations on a smaller scale. While the downbeat is the strongest beat in a measure, any note that falls on the beat is stronger than the other parts of the beat. Notes that do not fall on the beats are called offbeats.

Example 7.1.6. Weighted parts of beats

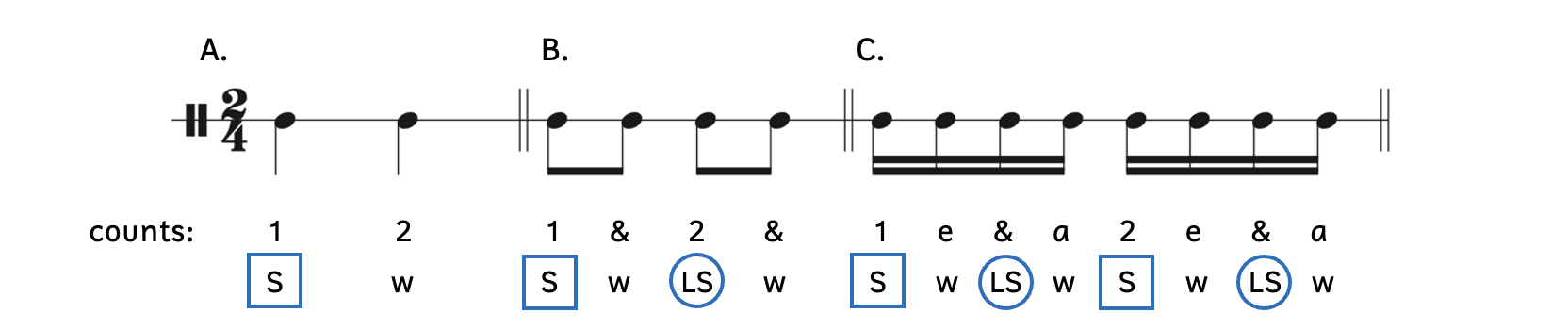
• Example 7.1.6A: At the beat level, beat 1 (in a blue box) is stronger than beat 2.
• Example 7.1.6B: At the division level, beat 1 is stronger than beat 2.
  • However, beat 2 (in a blue circle) is stronger than the final eighth note of beat 2, which is an offbeat.
• Example 7.1.6C: At the subdivision level, beat 1 is stronger than beat 2.
  • However, beat 2 is stronger than the final three sixteenth notes of beat 2.
  • In addition, the “&” of beat 2 is stronger than the final sixteenth note of beat 2.

Example 7.1.7 illustrates syncopations that occur on the offbeats (weak part of beats), rather than on weak beats.

Example 7.1.7. Offbeat syncopations: Suppé^[4], Overture to Poet and Peasant

In Example 7.1.7, Suppé’s melody falls on the offbeats for five bars.

• Notice how the melody (indicated by the blue arrows) falls between the beats written above. Although there are no accent markings, the notes fall on the offbeats and are held out. This creates more emphasis on the offbeats.
• The regular (unsyncopated) rhythm resumes at measures 116 and 118, but almost seem as if they are syncopated.

Many forms of dance music utilize syncopation. In Example 7.1.8, Guerreiro makes use of syncopation in a tango.

Example 7.1.8. Guerreiro, “Saude e…dinheiro” (“Health and…Money”)

• Like Example 7.1.7, Example 7.1.8 does not contain accent markings. Instead, notice where the longer note values of eighth notes occur: In both hands, they often fall in between beats.
• The two eighth notes in beat two of the left hand ground the meter and steadily reinforce the simple duple beat. This recurring pattern of offbeat longer note values creates syncopation.

An influencer of jazz, ragtime is also filled with syncopated rhythms (Example 7.1.9).

Example 7.1.9. Joplin^[5], “The Easy Winners”

In Example 7.1.9, there are two levels of syncopation. The syncopations discussed in this section are marked with asterisks.

• In measure 5, the quarter note falls on the second eighth of beat one (i.e., on the “and” of beat one).
• In measure 6 and 7, the first eighth note value falls on the second sixteenth of the beat (i.e., the “ee” of beat one).
• In measure 6, the second eighth note value falls on the second eighth of beat two.
• Across the bar line from measure 7 to measure 8, a note value equal to an entire measure plus a sixteenth note falls on the fourth sixteenth note of beat two (i.e., on the “uh” of beat two).
  • There are two “voices” in this example for piano. Notice that in the treble clef, one voice has stems that only point down, while the other voice has stems that only point up. This allows the first voice to be held the entire bar in measure 8 while the second voice begins an anacrusis into the next bar.

Three types of syncopation occur in Example 7.1.9 (syncopations on “and,” “ee,” and “uh”). Joplin makes the syncopations sound natural and not rhythmically disjunct by keeping constant eighth notes in the left hand, reinforcing the simple duple meter.

Syncopations can also occur in compound meters (Example 7.1.10).

Example 7.1.10. Offbeat syncopations: Röntgen-Maier^[6], Violin Sonata in B Minor, i – Allegro

• Example 7.1.10 is in 6/8, which is a compound meter.
• The violin plays the rhythm of the division (i.e., three eighth notes). However, rather than the beat being accented, the last (third) note of the division (an offbeat) is marked with a sforzando symbol resulting in syncopations. These syncopations are labeled with arrows.
• To support the syncopations in the violin, the piano also has sforzandi on the last eighth note offbeats.

Directions:

• Circle all syncopations in the following examples.
• How does the composer place emphasis on the syncopations?

1. de Gardéev^[7], Rumänisches Charakterstück, Op. 44

2. Szymanowska^[8], Prelude No. 1

3. Gabriel^[9], “Only”

Click here to watch the tutorial.

7.2  BORROWED DIVISION: TRIPLETS

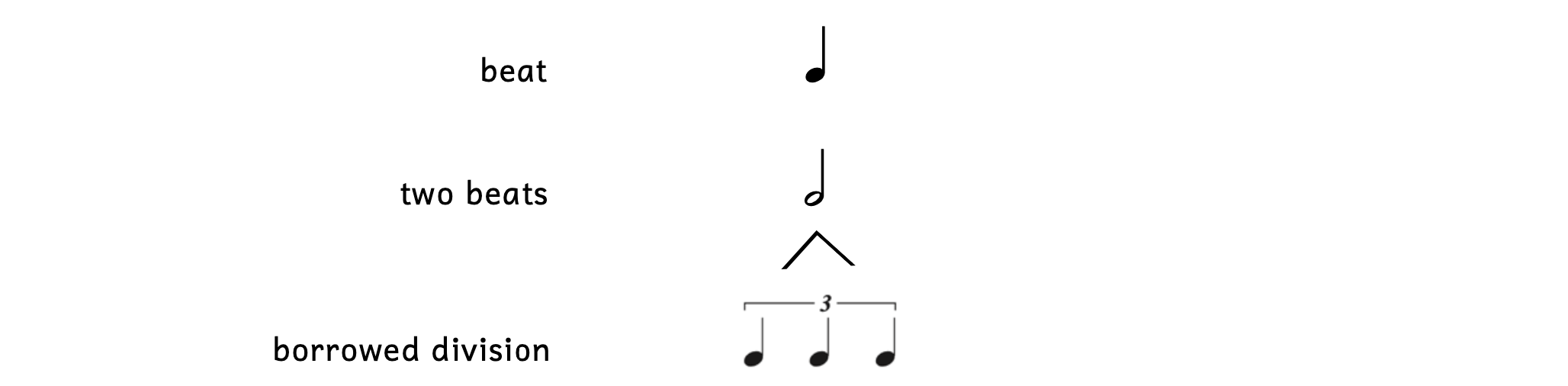
We learned that simple meters have beats that are evenly divided into two and compound meters have dotted beats that are equally divided into three. Sometimes, a simple meter will equally divide its beat into three and a compound meter will evenly divide its beat into two. When this occurs, it is called borrowed division.

Example 7.2.1. Borrowed division

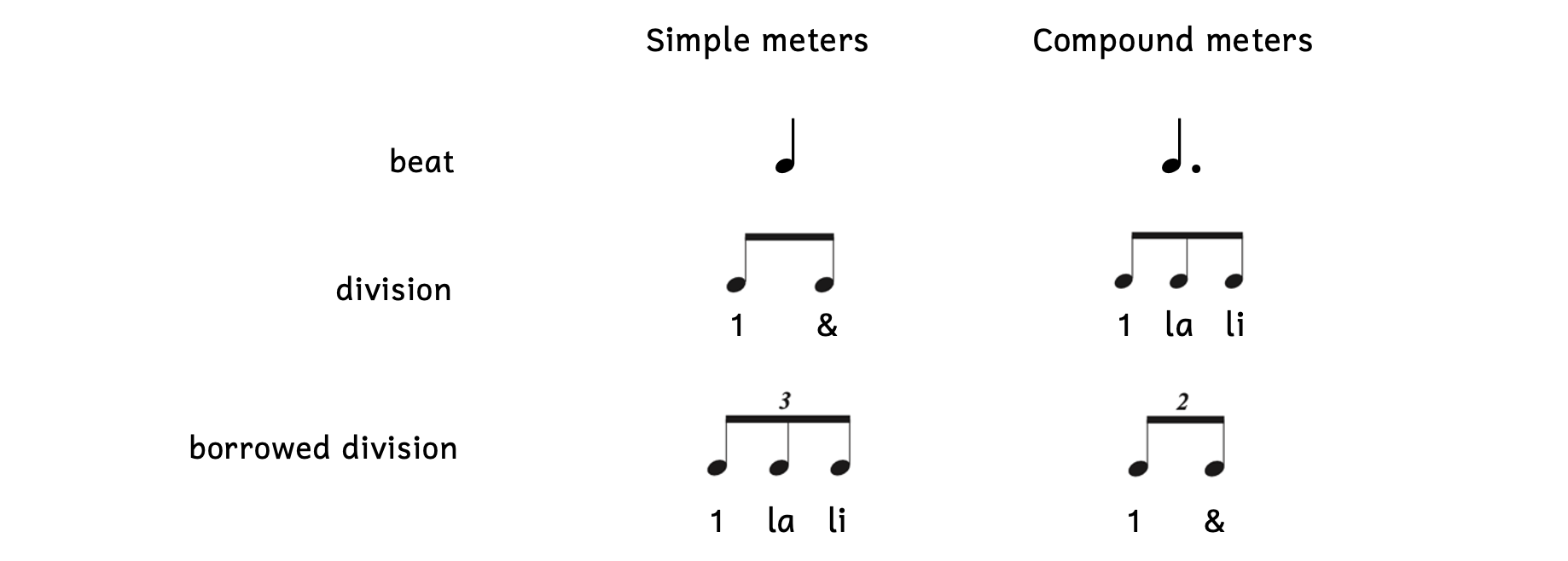
Borrowed division can occur in simple meters or compound meters. When any beat is not divided into its typical division or subdivision, it is called a tuplet.

When you equally divide a beat (without a dot) into three, the tuplet is called a triplet. The most important thing to remember when writing triplets is that you must include the number “3.” Otherwise, you are simply writing three notes.

Remember that a triplet is a type of borrowed division. This means that the note value of the division stays the same. In simple meters, rather than the beat dividing equally into two, a triplet will use the same note value as the division but there will be three notes instead of two.

Example 7.2.2. Triplet at the beat level

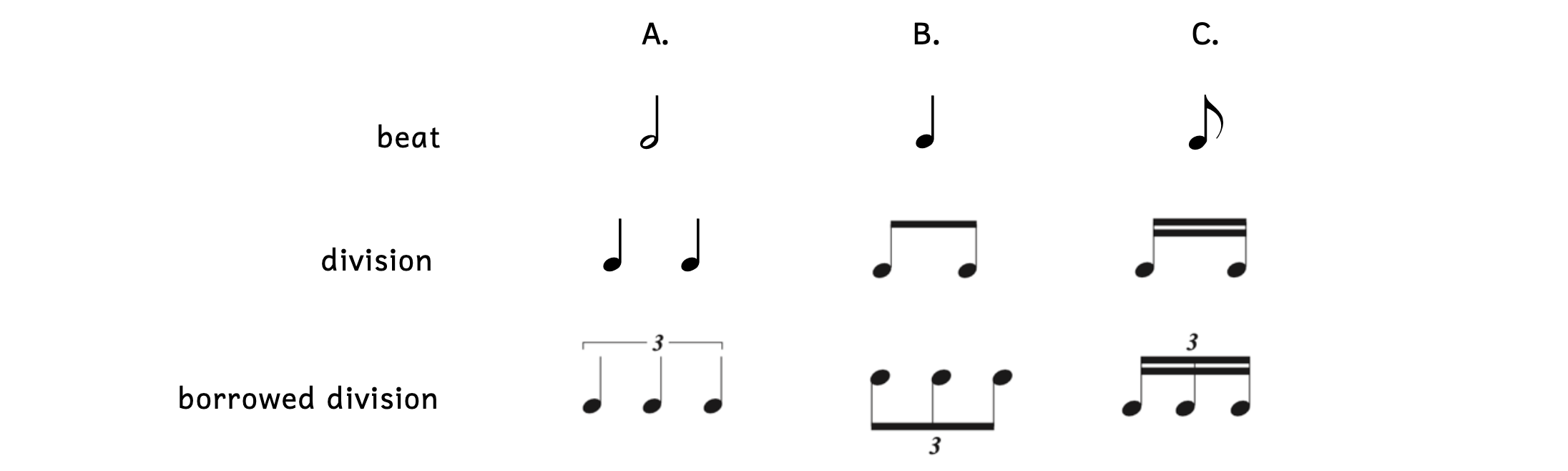
• Example 7.2.2A:
  • The beat is a half note.
  • The division is two quarter notes. Therefore, the borrowed division is three quarter-note triplets.
  • When there is no beam, add a bracket with the number “3.” Write the “3” on the stem side (opposite the notehead).
• Example 7.2.2B:
  • The beat is a quarter note.
  • The division is two eighth notes. Therefore, the borrowed division is three eighth-note triplets.
  • The stems are pointing down so the number “3” is added to the bottom (opposite the notehead). Because there is a beam, an added bracket is not necessary.
• Example 7.2.2C:
  • The beat is an eighth note.
  • The division is two sixteenth notes. Therefore, the borrowed division is three sixteenth-note triplets.
  • Because sixteenth notes have two flags, there are two beams. The number “3” is on the stem side (opposite the notehead). A bracket is not necessary.

Writing triplets is fairly simple if you remember two steps:

1. Write the division of the beat (i.e., two of the notes that equally divide into the beat).
2. Change the division of two into a division of three and add the number “3” on the stem side. If there is no beam, add a bracket.

Examples 7.2.3 and 7.2.4 show how to add triplets in different time signatures.

Example 7.2.3. Adding a triplet where a quarter note equals one beat

• Example 7.2.3A: Directions ask to add a triplet in beat two.
• Example 7.2.3B: First, figure out the beat’s division. A quarter note equals two eighth notes.
• Example 7.2.3C: Because the division is two eighth notes, the triplet would be three eighth notes. Since the three eighth notes are already beamed together, you would only need to add the number “3” on the stem side.
• Example 7.2.3D: In this example, the number “3” is not written. What results is too many beats: 3.5 beats in the time signature of 3/4.

Example 7.2.4. Adding a triplet where a half note equals one beat

• Example 7.2.4A: Directions ask to add a triplet in beat two.
• Example 7.2.4B: First, figure out the beat’s division. A half note equals two quarter notes.
• Example 7.2.4C: Because the division is two quarter notes, the triplet would be three quarter notes. Since the three quarters notes are not beamed together, you would need to add a bracket on the stem side and add the number “3.”
• Example 7.2.4D: In this example, the number “3” is not written. What results is too many beats: 2.5 beats in cut time.

Triplets are easy to spot because they will usually include the number “3.”

Example 7.2.5. Triplets: Rossini^[10], The Thieving Magpie, Overture

• In 3/4, the quarter note receives one beat and the division is two eighth notes. Beats are labeled with the blue square brackets.
• The division is marked in the second violins, and also occurs in the cellos and double basses, with an eighth note and eighth rest.
• Triplets appear in the first violins and violas, playing an octave apart. The division of three, which is normally found in compound meters, is used in this simple meter as triplets.

You may come across triplets in your music that do not have “3” written above or below. While this is acceptable for published scores, we will always be including the “3” when we write triplets.

Example 7.2.6. Implied triplets: Le Beau^[11], Theme and Variations, Op. 3, No. 7

In Example 7.2.6, the first and third beat of each measure have triplets although the “3” is not written. Musicians should realize that because of the beaming, triplets (three eighth notes beamed together) occur on the first and third beats while the division (two eighth notes beamed together) occurs on the second and fourth beats.

Any time a note (as opposed to a dotted note) equally divides into three, it forms a triplet. This includes notes that are part of the division (as opposed to the beat).

Example 7.2.7. Triplets at the division level

• Example 7.2.7A: Each eighth note in the division is equally divided into two sixteenth notes in the subdivision.
• Example 7.2.7B: The second eighth note in the division is equally divided into three sixteenth notes, resulting in a triplet.
  • This triplet is not equal to the beat; instead, it is equal to one of the divisions.

Example 7.2.8 illustrates a triplet dividing a division (rather than the beat).

Example 7.2.8. Triplets: Chopin^[12], Polonaise, Op. 40, No. 1

• In 3/4, the quarter note receives one beat and the division is two eighth notes. Beats are labeled with the blue square brackets.
• In both examples with square brackets, the second eighth note is subdivided into a sixteenth-note triplet.
  • The sixteenth-note triplet is equal to two sixteenth notes, which equals one eighth note.
  • Put together with the first eighth note, the eighth note and sixteenth-note triplets complete one beat.

Triplets can also be found in compound meters, but never to divide the beat since the beat is a dotted note and already divides equally into three. In compound meters, triplets will occur within the division of the beat (Example 7.2.9).

Example 7.2.9. Triplets: de la Hye^[13], Le corsaire rouge

• In 6/8, the dotted quarter note receives one beat and the division is three eighth notes.
• On the first beat of measure 13, the division of three eighth notes is clear.
• On the second beat of measure 13, the first eighth note is subdivided into sixteenth-note triplets.

Although 6/8 is a compound meter, we see triplets in Example 7.2.9. However, the triplets are not divisions of the beat (which are dotted notes) but rather, divisions of the division (which are not dotted notes).

Triplets can also be worth more than one beat.

Example 7.2.10. Triplets of longer values than one beat.

In Example 7.2.10, the quarter note is equal to one beat, which means the half note is equal to two beats. When the half note is equally divided into three quarter notes (instead of two), this becomes a quarter-note triplet and is worth two beats. We can see the triplet from Example 7.2.10 in context in Example 7.2.11.

Example 7.2.11. Triplet: Smyth^[14], Fête Galante: A Dance-Dream in One Act

• In 2/4, a half note fills an entire measure and can be equally divided into two quarter notes, as seen in measure 2.
• Just as two quarter notes fill a measure, three quarter-note triplets also fill a measure (measure 3).

Example 7.2.12 illustrates another triplet that is worth an entire measure.

Ex. 7.2.12. Triplet: Villa-Lobos^[15], A prólo do bébé, “Moreninha”

• In 4/4, a whole note fills an entire measure and can be equally divided into two half notes.
• Since two half notes fill a measure, three half-note triplets also fill an entire measure.

Whether the triplet is equal to a beat, half a beat, or multiple beats, always use the same technique when writing triplets: Determine what would divide the value into two and apply that note value to a triplet.

Directions:

• Write the borrowed division.

Click here to watch the tutorial.

Directions:

• Based on the given note that equals one beat, write how many beats or how much of one beat the following triplets are worth.

Click here to watch the tutorial.

Directions:

• Identify all triplets and write how many beats or how much of a beat each triplet is worth.
  • Remember that for published scores, the number “3” can be left out for triplets.

1. Macfarren^[16], “Bonnie Scotland”

2. Mayer^[17], Valse, Op. 32

3. Virgil^[18], Barchetta, Op. 23, No. 1

Click here to watch the tutorial.

7.3  OTHER TUPLETS

Triplets are used when a note (not a dotted note) equally divides into three. Dotted notes already divide evenly into three. When you equally divide a dotted note into two, this tuplet is called a duplet. The most important thing to remember when writing duplets is that you must include the number “2.” Otherwise, you are simply writing two notes.

Example 7.3.1. Duplet

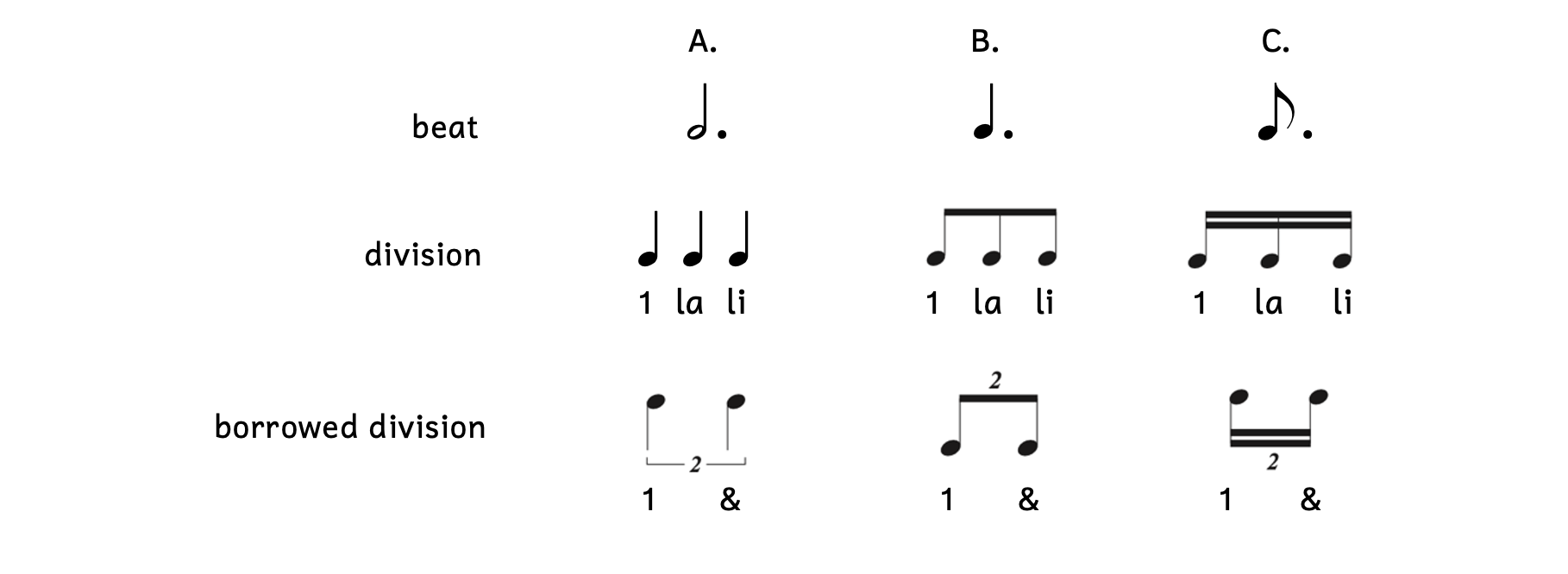
• Example 7.3.1A: The dotted half note receives the beat.
  • The division is three quarter notes. Therefore, the borrowed division is two quarter-note duplets.
  • When there is no beam, add a bracket with the number “2.” Write the “2” on the stem side (opposite the notehead).
• Example 7.3.1B: The dotted quarter note receives the beat.
  • The division is three eighth notes. Therefore, the borrowed division is two eighth-note duplets.
  • The stems are pointing up so the number “2” is added to the top (opposite the notehead). Because there is a beam, an added bracket is not necessary.
• Example 7.3.1C: The dotted eighth note receives the beat.
  • The division is three sixteenth notes. Therefore, the borrowed division is two sixteenth-note duplets.
  • Because sixteenth notes have two flags, there are two beams. The number “2” is on the stem side (opposite the notehead). An added bracket is not necessary.

Writing duplets is fairly simple if you remember two steps:

1. Write the division of the beat (i.e., three of the notes that equally divide into the beat).
2. Change the division of three into a division of two and add the number “2” on the stem side. If there is no beam, add a bracket.

Example 7.3.2. Adding a duplet where a dotted quarter note equals one beat

• Example 7.3.2A: Directions ask to add a duplet in beat 2.
• Example 7.3.2B: First, figure out the beat’s division. A dotted quarter note equals three eighth notes.
• Example 7.3.2C: Because the division is three eighth notes, the duplet would be two eighth notes. Since the two eighth notes are already beamed together, you would only need to add the number “2” on the stem side.
• Example 7.3.2D: In this example, the number “2” is not written. What results is not enough beats: the measure is one eighth note short.

Duplets are not as common as triplets, but are still found in the repertoire.

Example 7.3.3. Duplets: Debussy^[19], Suite bergamasque, “Clair de lune”

• In 9/8, the dotted quarter note receives one beat and the division is three eighth notes. Beats are labeled with the blue square brackets.
• The first beat of measure 3 clearly shows the division of three eighth notes.
• The next two beats of measure 3 are duplets, as two eighth notes equally divide the dotted quarter-note beat.

Sometimes composers will use a tuplet in one part while using the regular division (or subdivision) in another part. This occurrence is called polyrhythm (also referred to as cross rhythm).

Example 7.3.4. Polyrhythm: Rogers^[20], Violin Sonata in D Minor, op. 25, iii – Allegro giojoso

• In 6/4, the dotted half note receives one beat and the division is three quarter notes. Beats are labeled with the blue square brackets.
• The piano performs the typical division of three quarter notes per beat.
• At the same time, in measure 90, the violin performs duplets (two quarter notes equal one beat).
• Since these rhythms are occurring at the same time, it creates a polyrhythm.
• Notice that in both the violin part and the piano part, there are still two beats per measure. It is only the divisions that are different.

Polyrhythms can last longer than a measure or two. Indeed, when the polyrhythm occurs throughout an entire movement, composers may simply change the time signature as Bach does in Example 7.3.5.

Example 7.3.5. Polyrhythm with different time signatures: Bach^[21], Herz und Mund und Tat und Leben, (Heart and Mouth and Deed and Life), BWV 147, “Jesus bleibet meine Freunde” (“Jesus Shall Remain My Joy”)

• The melody occurs in the oboes and first violins in a compound triple meter (9/8).
• At the same time, the other instruments have the time signature of a simple triple meter (3/4).
• Rather than writing triplets each time, Bach simply changed the time signature of the oboes and first violins to 9/8.
• This is an example of polyrhythm because the compound triple and simple triple time signatures occur simultaneously. Both meters have three beats per measure; however, the divisions differ.

In Example 7.3.6, Smyth uses polyrhythm and also combines two duplets to form a quadruplet, or a division of four.

Example 7.3.6. Duplets and quadruplets: Smyth, String Quartet in E Minor, i – Allegretto lirico

• The second violin and viola strongly maintain the simple duple meter of 6/8. In addition to the divisions of three, each beat is accented.
• On the third eighth note where the second violin and viola have rests, the cello enters with a syncopated eighth note tied to a quarter note to fill the meter’s division of three.
• The first violin plays a duplet in measures 226 and 229. The two eighth notes equally divide the beat of the dotted quarter note.
• In measure 228, two duplets combine to form a quadruplet. Unlike the duplet, which filled the space of one beat, the quadruplet fills the space of two beats (or one measure).

The quadruplet in Example 7.3.6 was not a subdivision of the beat; rather, the quadruplet in bar 228 merged two duplets in a row, where each duplet is a borrowed division of the beat. However, music can also use borrowed subdivisions (Example 7.3.7).

Example 7.3.7. Sextuplet: Schubert^[22], “Ave Maria”

• • In common time, the quarter note receives one beat and the subdivision is four sixteenth notes.
  • The treble clef of the piano accompaniment is divided equally into six sixteenth notes, forming sextuplets. Because the subdivision of six resembles the subdivision of a dotted quarter note beat, the sextuplet is an example of borrowed subdivision.
  • In the voice part, the sixteenth notes imply a regular subdivision of four. As a result, polyrhythm occurs.

In addition to borrowed divisions and borrowed subdivisions, beats can be divided into any number (within reasons). In Example 7.3.8, Massanet divides the quarter note beat into three and into five.

Example 7.3.8. Quintuplet: Massanet^[23], Méditation from Thaïs

• In common time, the quarter note receives one beat, the division is two eighth notes, and the subdivision is four sixteenth notes.
• In the first bar, the violin performs an eighth-note triplet, where three eighth notes equal one beat.
• In measure 3, five sixteenth notes equal one beat: this is a quintuplet.

A quintuplet is not a type of borrowed division (three eighth notes) or a type of borrowed subdivision (six sixteenth notes), but is a type of tuplet. Squeezing five sixteenth notes into one beat is a different type of division than the typical division (two eighth notes) or typical subdivision (four sixteenth notes). Because a quintuplet of five is closer to the four-sixteenth-note division, the note values used for the quintuplet are sixteenth notes (rather than eighth notes).

A beat can be divided into any number of notes. Although each type of tuplet technically has a name (e.g., a beat divided into nine is called a nonuplet), we will only be using the most common divisions:

• Triplet: borrowed division in simple meters
• Duplet: borrowed division in compound meters
• Sextuplet: borrowed subdivision in simple meters
• Quadruplet: borrowed subdivision in compound meters
• Quintuplet: beat divided equally into five parts
• Septuplet: beat divided equally into seven parts

As a division of seven, the tuplets in Example 7.3.9 are septuplets. What type of note value does Le Beau use?

Example 7.3.9. Septuplets: Le Beau, Prelude, Op. 12, No. 1

Le Beau uses sixty-fourth notes. We can break it down to see why this is the correct note value. The septuplet fills in half a beat.

• One quarter note per beat or one eighth note per half a beat
• Two sixteenth notes per half a beat
• Four thirty-second notes per half a beat
• Eight sixty-fourth notes per half a beat

Since eight sixty-fourth notes is closest to the division of seven, the note values used are sixty-fourth notes.

The next example shows how extreme other divisions can be.

Example 7.3.10. Other tuplets: Szymanowska, Fantasie for the Piano

• In measure 2, the value of one sixteenth note is divided equally into twelve.
• In measure 3, the value of one sixteenth note is divided equally into eleven.

Although a division of 11 can be called a “undecuplet” and a division of 12 can be called a “dodecuplet,” for numbers greater than eight, it is more common to simply call these larger tuplets the number of the division plus the word “tuplet.” In Example 7.3.10, the first tuplet is more commonly called a “11-tuplet” and the second tuplet is called a “12-tuplet.”

As you can see, beats (or even part of a beat) can be equally divided into any number of parts (within reason).

Directions:

• Write the borrowed division.

Click here to watch the tutorial.

Directions:

• Based on the given note that equals one beat, write how many beats or how much of one beat the following tuplets are worth.

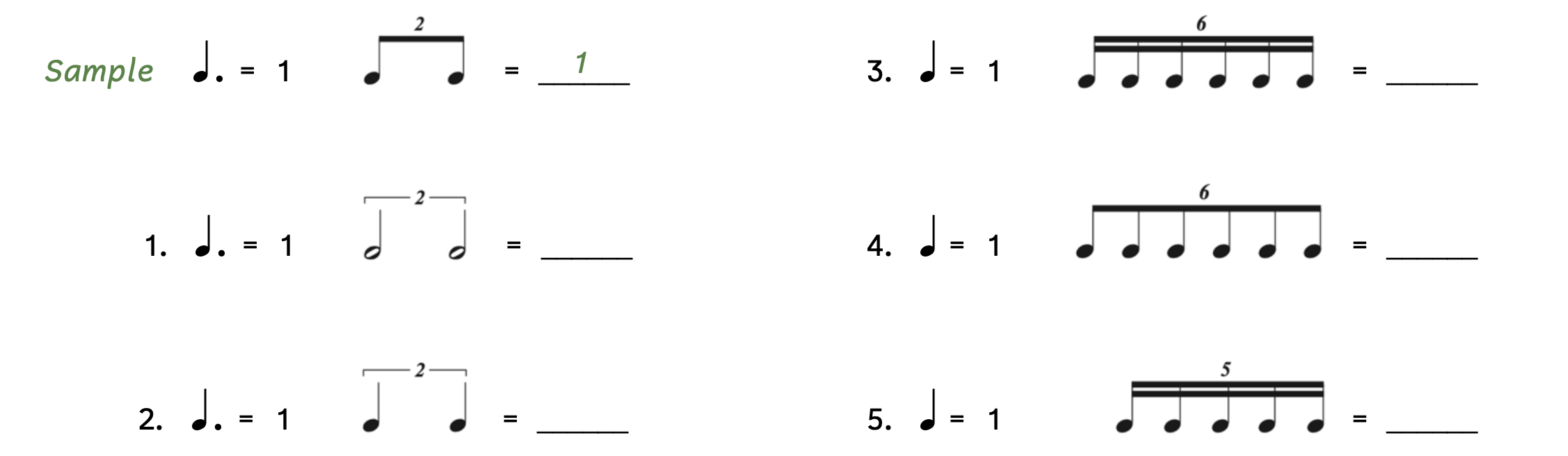
Click here to watch the tutorial.

Directions:

• Identify all tuplets. Write how many beats or how much of a beat each tuplet is worth.

1. Rothschild^[24], “Les Papillons”

2. Savage^[25], Six Easy Lessons for the Harpsichord or Pianoforte, Sonata No. 5, i – Moderato

3. Milanollo-Parmentier^[26], Lamento, Op. 7

4. Grandval^[27], Mazeppa, Act 2, Scene 6

Click here to watch the tutorial.

7.4  OTHER METERS

The time signature of 3/4 is an example of a triple meter: there are three beats per measure and the downbeat has the strongest accent (Example 7.4.1).

Example 7.4.1. Typical triple meter

Example 7.4.1 shows that there are three beats per measure and the accented downbeats are boxed.

Sometimes composers will temporarily shift the three beats per measure to two beats per measure, resulting in a hemiola. Although the accents change, it is important that the pulse of the beat does not change (Example 7.4.2).

Example 7.4.12 Hemiola

• In measure 1, there are three beats per measure and the downbeat (in blue boxes) receives the strongest accent.
• In measures 2-3, accents occur every two beats (in blue) instead of every three beats. This creates a hemiola.
• In measure 4, the typical accent pattern of three beats per measure returns.

Example 7.4.3 shows how Example 7.4.2 sounds.

Example 7.4.3. How a hemiola sounds

Examples 7.4.2 and 7.4.3 sound the same. The quarter note beat stays constant throughout. The hemiola becomes clear when the time signature and bar lines change. Mozart writes a hemiola in Example 7.4.4.

Example 7.4.4. Hemiola in Mozart^[28], Piano Sonata No. 12 in F Major, K. 332, i – Allegro

• In measures 62-63, the triple meter is blatant, as Mozart marks the accented downbeats with forte. Beats two and three immediately drop down to piano.
• On the third beat of measure 64, the pattern is broken with a surprising forte on beat three.
• Two beats later, on the second beat of measure 65, the next forte occurs.
• In measure 66, the original triple meter resumes.

In Example 7.4.4, the triple meter switches temporarily to 2/4, resulting in a hemiola. With the contrast of dynamics, the hemiola is made even more clear.

When a hemiola occurs at the same time as the meter that is written, it created a polymeter. While a polyrhythm retains the beat while different divisions occur simultaneously, a polymeter is when two meters occur simultaneously. Observe the following melody by Johann Strauss.

Example 7.4.5. Two beats per measure: Strauss^[29], Frülingsstimmen Waltz, Op. 410

The melody in Example 7.4.5 clearly shows two beats per measure with the downbeat receiving the accent. However, this is not what Strauss wrote. Strauss wrote this duple melody over a triple-meter accompaniment (Example 7.4.6).

Example 7.4.6. Polymeter with hemiola: Strauss, Frülingsstimmen (Voices of Spring) Waltz, op. 410

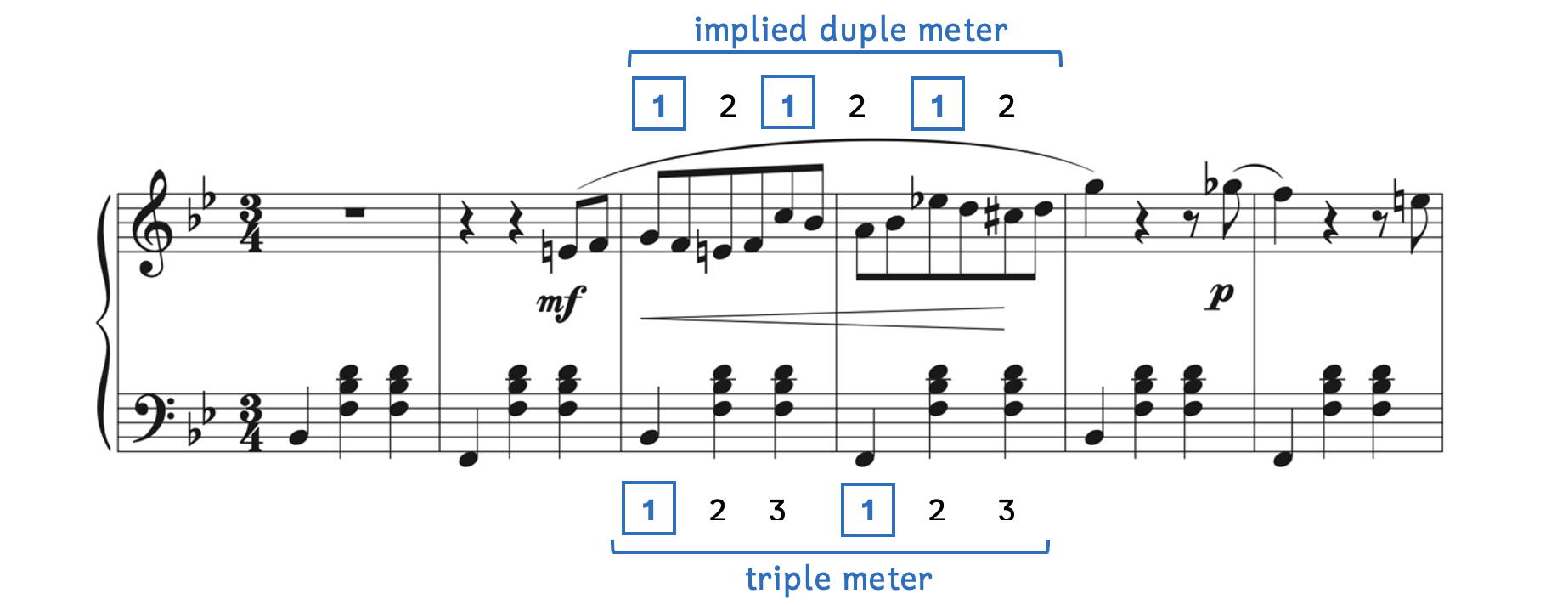
• The right hand plays the melody from Example 7.4.5, which implies a duple meter (accents every two beats).
• At the same time, the left hand plays an accompaniment in triple meter (accents every three beats).

There is polymeter in Example 7.4.6 because measures 3-4 of the right hand has accents every two beats, while the left hand has accents every three beats.

Johannes Brahms is well known for his use of hemiolas, polyrhythm, and polymeter. It is important to establish a strong sense of meter before applying any of these elements. In Example 7.4.7, a regular compound duple meter is set at the start.

Example 7.4.7. Established meter: Brahms^[30], Intermezzo, Op. 119, No. 3

The time signature of 6/8 is a compound duple meter: There are two beats per measure and the beat is equally divided into three. The meter is clearly set at the start. Later in the Intermezzo, Brahms applies a shift of meter (Example 7.4.8).

Example 7.4.8. Shift of meter: Brahms, Intermezzo, Op. 119, No. 3

• Measure 45 is similar to the start of the piece, implying a compound duple meter.
• On the second beat of measure 47, the meter suddenly shifts to what sounds like 3/4. While the eighth note division remains constant, they are now grouped into two instead of three.
• The last half of measure 48 is filled with a sixteenth-note quintuplet and eighth note.

In Example 7.4.8, metrical accents are questionable. This is best achieved by preparing the listener with a clear pattern of accented beats from a regular meter.

In addition to the traditional time signatures we have learned, there are also irregular meters. Irregular meters include any time signatures that are not duple, triple, or quadruple meters such as 5/4.

Example 7.4.9. Irregular meter: Holst^[31], The Planets, Op. 32, “Mars, the Bringer of War”

• Holst begins this movement from The Planets in 5/4, an irregular meter.
• This would be classified as a simple meter, as the beat is a quarter note (and not a dotted note) that divides equally into two. When the quarter-note beat is equally divided into three, the number “3” is used to imply borrowed division. 

Irregular meters have time signatures where the top number is not typical, such as “5” or “7.” In addition, irregular meters can have time signatures that show how the beats are divided in each measure, called composite meters or asymmetrical meters. Composite meters combine simple divisions of two and compound divisions of three but the divisions remain constant. This means that the beats are not symmetrical.

Ex. 7.4.10. Composite meter: Reicha^[32], Fugue, Op. 36, No. 20

• The time signature is a composite meter. It shows that each measure is divided into three eighth notes, then two eighth notes.
• Notice how the beaming follows the time signature. In measures 2 and 4, the first three eighth notes are beamed together and in measures 1 and 3, the last two eighth notes are beamed together.

Whereas Example 7.4.9 in 5/4 was an example of a simple meter, Example 7.4.10 is more like a compound meter. The bottom number does not refer to the beat, but rather, the division. There are two beats per measure in Example 7.4.10, although the beats are not even: The beats sound like the music is limping as the first beat is longer than the second beat by an eighth note.

Example 7.4.11 shows another instance of a composite meter.

Example 7.4.11. Composite meter: Bartók^[33], Six Dances in Bulgarian Rhythm, No. 2

• The composite meter keeps a constant eighth note, but the accents change.
  • In the first two beats, every other eighth note creates an accent.
  • In the third beat, three eighth notes form an accent.
• The beats (accents) are clear with the beaming: 2 + 2 + 3.

Time signatures can also change throughout a work, called changing meters.

Example 7.4.12. Changing meters: Mussorgsky^[34], Pictures at an Exhibition, Promenade

In the opening of Mussorgsky’s Pictures at an Exhibition, he alternates between 5/4 and 6/4. The quarter note remains constant and the time signature changes.

Directions:

• Describe what is occurring metrically in the following examples.

1. Brahms, Horn Trio, Op. 40, iv – Finale: Allegro con brio

2. Tchaikovsky^[35], Symphony No. 6, Op. 74, ii – Allegro con grazia

3. Villa-Lobos, A prólo do bébé, “O polichinelo”

Click here to watch the tutorial.

7.5  ANALYSIS: BRAHMS, SCHICKSALSLIED

As previously mentioned, Johannes Brahms is well known for his use of hemiolas. Observe the dramatic use of a hemiola in Example 7.5.1.

Example 7.5.1. Hemiola: Brahms, Schicksalslied, Op. 54

Listen to Example 7.5.1 while clapping the beat. Accent all the beats that are boxed.

• The first six measures (measures 140-145) have three beats per measure. The simple triple beat is clearly established.
• In measures 146-152, a hemiola occurs as the vocalists’ parts alternate between a note and a rest creating two-beat “measures.”
• In measure 154, the triple meter resumes after an entire measure of rest in measure 153.

The words and the music go hand in hand in Example 7.5.1.

• When the music is in a triple meter (measures 140-145), the choir sings, “blindly from one brief hour to another.”
• Then, during the hemiola (measures 146-152), the choir sings, “Like water from boulder to boulder flung downward.” Listen to the example: Do you hear how the music sounds like water is bouncing from one stone to the next?

Brahms uses word painting: when music attempts to sound like the meaning of the words. Brahms takes advantage of the hemiola to give a powerful musical representation of water skipping from rock to rock.

SUMMARY

• • 1. Syncopations are when weak beats or weak parts of beats are accented somewhat regularly.
    2. Borrowed division refers to when a beat (not a dotted beat) is evenly divided into three instead of two (called a triplet) or when a dotted beat is equally divided into two instead of three (called a duplet).
    3. A sextuplet is a type of borrowed subdivision when a beat (not a dotted beat) is subdivided into six instead of four.
    4. The generic term for any note being divided into any number that is not its division or subdivision is called a tuplet.
       • Triplets, duplets, and sextuplets are types of tuplets.
       • Although beats can be divided into any number (e.g., 11), the most common non-division tuplet is the quintuplet (beat divided equally into five).
    5. When a division and a tuplet occur simultaneously, a polyrhythm (or cross rhythm) occurs.
    6. A hemiola is when the meter temporarily shifts from three beats per measure to accents every two beats.
    7. Polymeter is when two implied time signatures occur simultaneously.
    8. Irregular meters include time signatures that are not typical simple and compound meters (e.g., 5/4).
       • A specific type of irregular meter is called a composite meter, which breaks down the division of a time signature. For example, the top number maybe be 3+2.
    9. Changing meters are when the time signature changes.

TERMS

• • • asymmetrical meters
    • augmentation
    • borrowed division
    • changing meter
    • composite meter
    • diminution
    • duplet
    • hemiola
    • irregular meter
    • offbeat
    • polymeter
    • polyrhythm (also cross rhythm)
    • quadruplet
    • quintuplet
    • septuplet
    • sextuplet
    • syncopation
    • triplet
    • tuplet